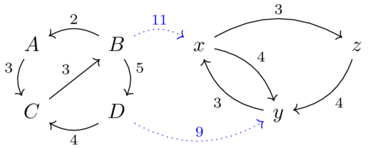
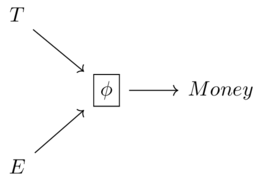
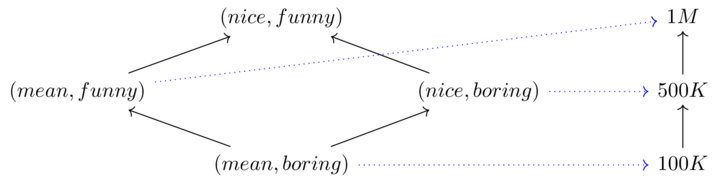
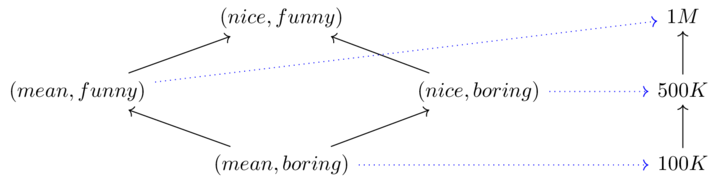
Feasibility relationships as Bool-profunctors(6)
Whenever you have 10 W of power, you also have 5 W (\(5 W \leq 10 W\))
The requirement that the feasibility relation map is monotone says that if \(x' \leq_X x\) and \(y \leq_Y y'\), then \(\phi(x,y) \leq_{Bool} \phi(x',y')\)
If x can be obtained from y, something easier to obtain than x can also be obtained from y
If x can be obtained from y, then x can be obtained from something harder to obtain than y
This chapter should make the following table clear:
Bool- Bool- Bool- Bool is a quantale, meaning it has all joins and a closure operation, \(\mathbb{B}\times\mathbb{B}\xrightarrow{\Rightarrow}\mathbb{B}\). The closure operation must satisfy \(b \land c \leq d\) iff \(b \leq (c \Rightarrow d)\). It is the fact that Bool is a quantale that makes this chapter work; we could alternatively use Cost and obtain the cost of obtaining \(x\) from \(y\), not just whether or not it’s possible.
Feasilibiliy relation(1)
A feasibility relation for preorder \(X\) given preorder \(Y\)
A monotone map \(X^{op}\times Y \xrightarrow{\phi} \mathbf{Bool}\)
Also denoted \(X \overset{\phi}\nrightarrow Y\)
Given \(x \in X, y \in Y\), if \(\phi(x,y)=true\) then we say x can be obtained from y
Linked by
- Can we build it: referenced
- Feasibility relationships as Bool-profunctors: referenced
- Feasibility relationships as Bool-profunctors: referenced
- Exercise 4-10: referenced
- Back to co-design diagrams: referenced
- Movie constraints: referenced
- Movie constraints: referenced
- Composing Bool-profunctors: referenced
- The categories V-Prof and Feas: referenced
Exercise 4-4(2)
Suppose we have the preorders \(X:=\boxed{monoid\rightarrow category \leftarrow preorder}, Y:=\boxed{nothing \rightarrow thisBook}\)
Draw the Hasse diagram for the preorder \(X^{op} \times Y\)
Write a profunctor \(X \overset{\phi}\nrightarrow Y\)
True means “my aunt can explain an x given y"
Interpret the fact that the preimage of true is an upper set in \(X^{op}\times Y\)
Solution(1)
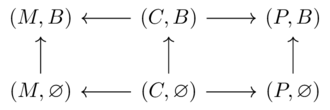
Let \(\phi((M,B))=\phi((P,B))=True\) else \(False\)
The preimage of true being an upper set is a consequence of monotone maps to Bool. The domain orders combinations by feasibility (\(x\leq y\) means x is easier than y), and the preimage being an upper set says that if my aunt can explain \(x\) given \(y\), then she can do something easier than \(x\) given \(y\) and can explain \(x\) with something with more explanatory power than \(y\).
Exercise 4-7(2)
Show that the Boolean \(\Rightarrow\) satsifies the requirements of a closure operator.
Solution(1)
This boils down to the tautology that \((a \land v) \implies w\) iff \(a \implies (v \implies w)\), where the last \(\implies\) comes from \(\multimap\) and the others come from \(\leq\).