Composing profunctors(4)
V-profunctor composition(1)
The composite \(\mathcal{X}\overset{\phi;\psi}\nrightarrow \mathcal{Z}\) of two \(\mathcal{V}\) profunctors, \(\mathcal{X}\overset{\phi}\nrightarrow\mathcal{Y}\) and \(\mathcal{Y}\overset{\psi}\nrightarrow\mathcal{Z}\)
\((\phi;\psi)(x,z) = \bigvee_Y(\phi(x,y)\otimes\psi(y,z))\)
Linked by
Composing Bool-profunctors(1)
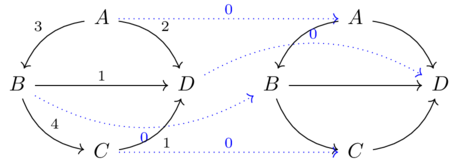
Need a formula for composing two feasibility relations in series.
Suppose \(P,Q,R\) are cities (preorders) and there are bridges (hence, feasibility matrices).
The feasibility matrices are:
\(\textcolor{blue}{\phi}\) a b c d e N T F T F F E T F T F T W T T T T F S T T T T T \(\textcolor{red}{\psi}\) x y a F T b T T c F T d T T e F F Feasibility from \(P\) to \(R\) means there is a way-point in Q which is both reachable from \(p \in P\) and can reach \(r \in R\).
Composition is a union \((\phi;\psi)(p,r):= \bigvee_Q \phi(p,q)\land \psi(q,r)\).
But this is tantamount to matrix multiplication which gives us the result matrix:
\(\phi;\psi\) x y N F T E F T W T T S T T
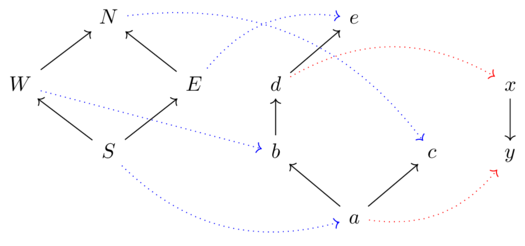
Exercise 4-22(2)
Consider the following Cost profunctors \(\textcolor{blue}{\phi},\textcolor{red}{\psi}\) \[\begin{tikzcd}[ampersand replacement=\&] A \arrow[d, "3"', bend right] \& B \arrow[l, "2"', bend right] \arrow[d, "5", bend left] \arrow[r, "11", blue, dotted, bend left] \& x \arrow[rr, "3", bend left] \arrow[rd, "4", bend left] \& \& z \arrow[ld, "4", bend left] \arrow[r, "4", red,dotted, bend left] \arrow[rd, red, "4", dotted, bend right] \& p \arrow[r, "2", bend left] \& q \arrow[d, "2", bend left] \\ C \arrow[ru, "3"] \& D \arrow[l, "4", bend left] \arrow[rr, blue, "9", dotted, bend right] \& \& y \arrow[lu, "3", bend left] \arrow[rrr, red, "0", dotted, bend right=49] \& \& d \arrow[u, "1", bend left] \& r \arrow[l, "1", bend left] \end{tikzcd}\]
Fill in the matrix for the composite profunctor.
Solution(1)
| \(\phi;\psi\) | p | q | r | s |
|---|---|---|---|---|
| A | 23 | 25 | 21 | 22 |
| B | 17 | 19 | 15 | 16 |
| C | 20 | 22 | 18 | 19 |
| D | 11 | 13 | 9 | 10 |