Can we build it(1)
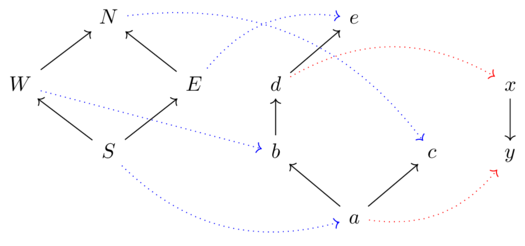
A large project is broken down into subprojects, each of which can be broken down into further subprojects.
Each subproject provides resources (or ‘functionalities’) but also requires resources.
There are interdependencies; if subteam A needs more space in order to provide a resource for B, B may need to use less space, causing a ripple effect.
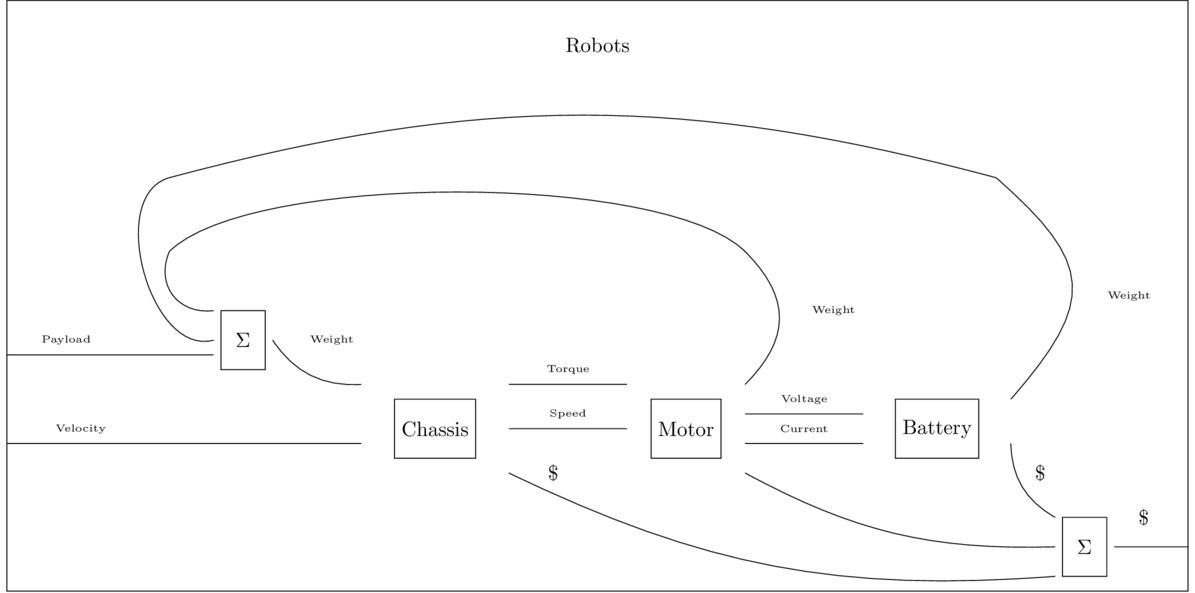
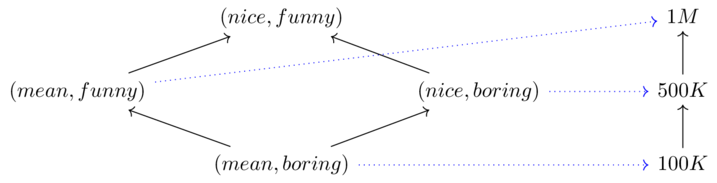
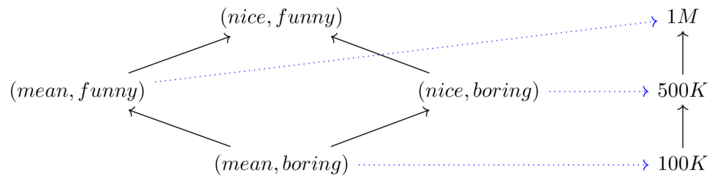
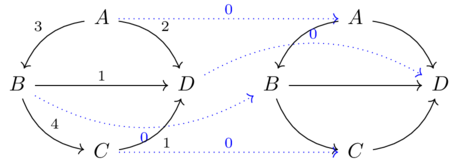
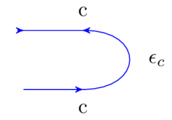
Codesign diagrams have wires which represent a preorder of resources.
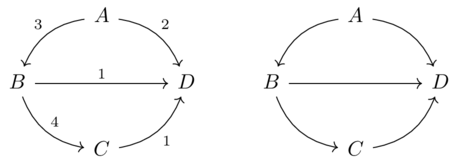
Boxes correspond to feasibility relations which match resource production with requirements
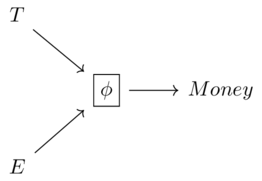
For every pair (p,r), where \(P\) is the preorder of resources to be produced and \(R\) is the preorder of resources to be required, the box says true or false for that pair.
I.e. “yes I can provide p given r" or “No, I cannot provide p given r"
I.e. Feasibility relations define a function \(P \times R \xrightarrow{\Phi}\mathbb{B}\) subject to some conditions
A co-design problem, represented by a co-design diagram, asks us to find the composite of some feasibility relations.