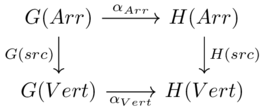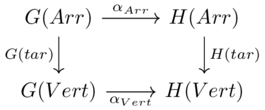The category of instances on a schema

An instance homomorphism between two database instances, \(\mathcal{C}\xrightarrow{I,J}\mathbf{Set}\)

• A natural transformation between the two functors representing the instances.

• \(\mathcal{C}\mathbf{Inst}:=\mathbf{Set}^\mathcal{C}\) denotes the functor category where these instance homomorphisms are the morphisms.

• The category of graphs as a functor category

• Schema for graphs: \(\mathbf{Gr}:=\boxed{\overset{Arr}\bullet \overset{src}{\underset{tar}{\rightrightarrows}}\overset{Vert}\bullet}\)

• A graph instance has a set of points and a set of arrows, each of which has a source and target.

• There is a bijection between graphs and Gr instances

• The objects of GrInst are graphs, the morphisms are graph homomorphisms (natural transformations between two Gr to Set functors)

  • Each graph homomorphism contains two components, which are morphisms in Set:

    1. ?\(G(Vert) \xrightarrow{\alpha_{vert}} H(vert)\)

    2. ?\(G(Arr) \xrightarrow{\alpha_{arr}} H(Arr)\)

  • Naturality conditions

    1. 

    2. 

• Consider the graphs \(G:=\boxed{\overset{1}\bullet \xrightarrow{a} \overset{2}\bullet \xrightarrow{b}\overset{3}\bullet}\) and \(H:=\boxed{\overset{4}\bullet \overset{d}{\underset{c}{\rightrightarrows}}\overset{5}\bullet\circlearrowleft e}\)

• The arrow table of their database instances are below:

• ?

  G	src	tar
  a	1	2
  b	2	3

• ?

  H	src	tar
  c	4	5
  d	4	5
  e	5	5

Linked by

• Exercise 3-64: referenced

Consider the graphs \(G,H\) from Example 3.63. We claim there is exactly one graph homomorphism such that \(\alpha_{Arr}(a)=d\). What is the other value of \(\alpha_{Arr}\), and what are the three values of \(\alpha_{Vert}\)?

Solution(1)

• We need \(2 \mapsto 5\), so the source of \(\alpha_{Arr}(b)\) must be \(5\) (there is only one arrow to pick, \(e\)).

• \(1 \mapsto 4,\ 2\mapsto 5,\ 3 \mapsto 5\)