Exercise 3-55

Let’s investigate why the functor category is actually a category.

  1. Figure out how to compose natural transformations \(F \xrightarrow{\alpha} G \xrightarrow{\beta}H\).

  2. Propose an identity natural transformation on any functor and check that it is unital.

Solution(1)

  1. The individual natural transformations satsifying the naturality condition makes the left and right squares commute, meaning the whole diagram commutes:

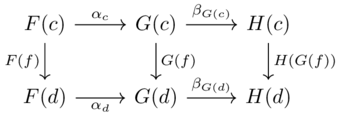
    • Thus the mapping from objects in \(F\)’s domain to morphisms in \(H\)’s codomain is given by \(G;\beta\).

  2. Mapping each object to its own identity morphism will satisfy the naturality condition (all four edges of the square become identity functions). This will enforce unitality.