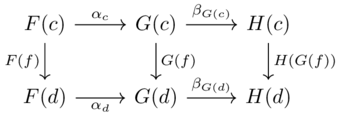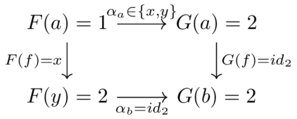Natural transformation(1)
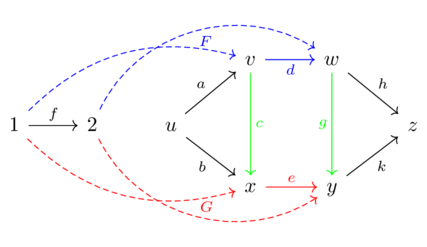
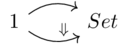
A natural transformation \(F \overset{a}\Rightarrow G\) between two functors (going from \(\mathcal{C}\) to \(\mathcal{D}\)).
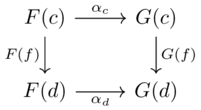
For each object \(c \in \mathcal{C}\), one specifies a morphism \(F(c)\xrightarrow{\alpha_c}G(c)\) in \(\mathcal{D}\) called the c-component of \(\alpha\)
These components must satisfy the naturality condition: for each morphism \(c \xrightarrow{f} d\) in \(\mathcal{C}\) we need \(F(f);\alpha_d=\alpha_c;G(f)\)
AKA this diagram should commute:
Linked by
- Functor category: referenced
- Small natural transformation example: referenced
- Natural transformation to unit: referenced
- Natural transformations between sequences: referenced
- Natural isomorphism of Bool-categories and preorders: referenced
- Exercise 3-55: referenced
- Exercise 3-55: referenced
- Solution: referenced
- Exercise 3-58: referenced
- Exercise 3-58: referenced
- Solution: referenced
- Instance homomorphism: referenced
- Grph as functor category: referenced