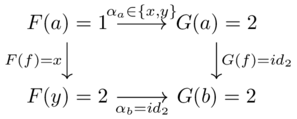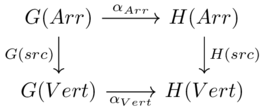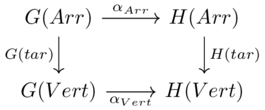Functors, natural transformations, and databases

Sets and functions as databases(1)
Functors(11)
Functor(1)
Example between small categories(1)

  • Between the free square category and the commutative square category, there is no functor from the commutative square category to the free square category which keeps the corners in the same place.

  • If we did this, we’d have \(F(f;h)=F(g;i)\) (since these are the same morphism).

  • The functor rules would allow us to break this up into \(F(f);F(h)=F(g);F(i)\) and we don’t have a choice for those mappings other than \(f;h=g;i\), something that is not true in the free square category.

Functor between preorders(1)

Functors between preorders are monotone maps. Morphisms in the source must map to sources in the target, so if \(a \leq_P b\), then we require \(F(a) \leq_Q F(b)\), which is tantamount to the monotone map constraint.

Exercise 3-37(2)

How many functors are there from 2 to 3?

Solution(1)

We are only concerned about where the objects go, since the target category is a thin category (there is no choice about which morphism is mapped to). Thus the functors are: 11, 22, 33, 12, 23, 13

Exercise 3-39(2)

Say where each of the 10 morphisms in the free square category are mapped to by a functor to the commutative square category (where \(Ob(F)\) maps each corner to the same corner).

Solution(1)

The four identity morphisms and four length-1 paths are trivially mapped to the the corresponding morphisms. Both length-2 paths in the free category are mapped to the same morphism, \(f;h\).

Exercise 3-40(2)

Consider \(\mathcal{C}=\boxed{\bullet \rightarrow \bullet}\) and \(\mathcal{D}=\boxed{\bullet \rightrightarrows \bullet}\). Give two functors that act the same on objects but differently on morphisms.

Solution(1)

Let the two functors map the left object to the left object and right object to the right object. The first functor maps the nontrivial morphism to the upper morphism in \(\mathcal{D}\), whereas the second maps it to the lower morphism.

Exercise 3-43(2)

  1. Given a category \(\mathcal{C}\), show that there exists a functor \(id_\mathcal{C}\) known as the identity functor on \(\mathcal{C}\)

  2. Show that given \(\mathcal{C}\xrightarrow{F}\mathcal{D}\) and \(\mathcal{D}\xrightarrow{G}\mathcal{E}\) we can define a new functor \(\mathcal{C}\xrightarrow{F;G}\mathcal{E}\) just by composing functions.

  3. Show that there is a category, let’s call it Cat where the objects are categories, morphisms are functors, and identities/composition are given as above.

Solution(1)

  1. Mapping objects and morphisms to themselves satsifies the functor constraints of preserving identities and composition.

  2. If \(F,G\) both independently preserve identity arrows, then composition of these will also preserve this. Also \(G(F(f;g))=G(F(f);F(g))=G(F(f));G(F(g))\) using the independent facts that \(F,G\) each preserve composition.

  3. Composition of identity functions do not change anything, so the identity functor (defined by identity function) will obey unitality. Because function composition is associative and functor composition is defined by this, we also satisfy that constraint.

Database instances as Set-valued functors(5)

Just like all sets are instances on the schema 1, all functions are instances on the schema 2.

Database instance(1)

A \(\mathcal{C}\) instance, where \(\mathcal{C}\) is a schema, i.e. a finitely-presented category.

A functor \(\mathcal{C} \xrightarrow{I} \mathbf{Set}\)

Linked by

Database instance example(1)

  • Consider the following category: \(\boxed{\overset{\bullet}{z}\circlearrowleft s\ \ \boxed{s;s = s}}\)

  • A functor from this category to Set is a set \(Z\) and a involution function \(Z \rightarrow Z\).

    • \(Z =\) natural numbers and a function sending everything to zero (zero is sent to zero)

    • \(Z =\) set of well-formed arithmetic expressions (e.g. \(12+(2*4)\)) and a function which evaluates to an integer (which itself is a well-formed expression). Evaluation on integers does nothing.

    • A function which sends numbers greater than 2 to their smallest prime factor (this is a no-op on the prime factors themselves).

Exercise 3-45(2)

For any functor \(\mathbf{1} \xrightarrow{F} \mathbf{Set}\) one can extract a set, \(F(1)\). Show that for any set \(S\) there is a functor \(\mathbf{1}\xrightarrow{F_S}\mathbf{Set}\) such that \(F_S(1)=S\)

Solution(1)

Define \(F_S\) to send the object of 1 to \(S\) and preserve identity morphisms. There is no nontrivial composition to enforce, so this is a valid functor.

Natural transformations(11)
Natural transformation(1)

A natural transformation \(F \overset{a}\Rightarrow G\) between two functors (going from \(\mathcal{C}\) to \(\mathcal{D}\)).

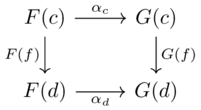
  • For each object \(c \in \mathcal{C}\), one specifies a morphism \(F(c)\xrightarrow{\alpha_c}G(c)\) in \(\mathcal{D}\) called the c-component of \(\alpha\)

  • These components must satisfy the naturality condition: for each morphism \(c \xrightarrow{f} d\) in \(\mathcal{C}\) we need \(F(f);\alpha_d=\alpha_c;G(f)\)

  • AKA this diagram should commute:

Linked by

Diagram(1)

A diagram \(\mathcal{D}\) in a category \(\mathcal{C}\)

  • A functor \(\mathcal{J}\xrightarrow{D}\mathcal{C}\) from any category \(\mathcal{J}\) called the indexing category of the diagram \(D\).

  • We say \(D\) commutes if \(D(f)=D(f')\) for every parallel pair of morphisms \(f,f'\) in \(\mathcal{J}\)

Functor category(1)

The functor category from categories \(\mathcal{C}\) to \(\mathcal{D}\)

\(\mathcal{D}^\mathcal{C}\) has all functors \(\mathcal{C} \rightarrow \mathcal{D}\) as objects and natural transformations as morphisms.

Linked by

Small natural transformation example(1)

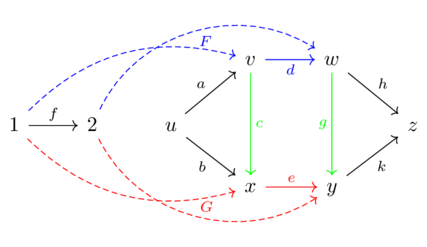
  • The natural transformation requires us to choose morphisms in the righthand category for each object in the lefthand category

  • The only choices to satisfy the naturality condition are \(c\) and \(g\).

Natural transformation to unit(1)

  • Just like sets are in bijection with functors \(\mathbf{1}\rightarrow\mathbf{Set}\), we can also associate natural transformations

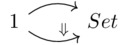
    with functions.

  • In the language of functor categories, this claim is to say \(\mathbf{Set}^1\) is equivalent to \(Set\).

Linked by

Natural transformations between sequences(1)

  • Any non-decreasing sequence of naturals can be identified with a functor \(\mathbb{N}\rightarrow \mathbb{N}\), considering the preorder of naturals as a category.

  • A natural transformation between two of these functors would require a component \(\alpha_n\) for each natural, which means a morphism from \(F_n \rightarrow G_n\). This exists iff \(F(n)\leq G(n)\).

  • Thus we can put a preorder structure over the monotone map of \(\mathbb{N} \rightarrow \mathbb{N}\) (this is a thin functor category \(\mathbb{N}^\mathbb{N}\)).

Natural isomorphism of Bool-categories and preorders(1)

  • There exists a category PrO which has preorders as objects and monotone maps as morphisms.

  • There exists a category *Bool-Cat* in which the objects are Bool-categories and morphisms are Bool-functors.

  • We call these categories equivalent because there exist functors \(\mathbf{PrO}\overset{F}{\underset{G}{\rightleftarrows}}\mathbf{BoolCat}\) such that there exist natural isomorphisms \(F;G \cong id_\mathbf{PrO}\) and \(G;F \cong id_\mathbf{Bool-Cat}\)

Exercise 3-55(2)

Let’s investigate why the functor category is actually a category.

  1. Figure out how to compose natural transformations \(F \xrightarrow{\alpha} G \xrightarrow{\beta}H\).

  2. Propose an identity natural transformation on any functor and check that it is unital.

Solution(1)

  1. The individual natural transformations satsifying the naturality condition makes the left and right squares commute, meaning the whole diagram commutes:

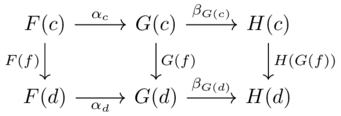
    • Thus the mapping from objects in \(F\)’s domain to morphisms in \(H\)’s codomain is given by \(G;\beta\).

  2. Mapping each object to its own identity morphism will satisfy the naturality condition (all four edges of the square become identity functions). This will enforce unitality.

Exercise 3-58(2)

Let \(\mathcal{C}\) be an arbitrary category and \(\mathcal{P}\) be a preorder thought of as a category. Are the following true?

  1. For any two functors \(\mathcal{C}\xrightarrow{F,G}\mathcal{P}\), there is at most one natural transformation \(F \rightarrow G\)

  2. For any two functors \(\mathcal{P}\xrightarrow{F,G}\mathcal{C}\), there is at most one natural transformation \(F \rightarrow G\)

Solution(1)

  1. This is true: there are no choices to be made for a natural transformation, given that for each morphism \(c\rightarrow d\) in \(\mathcal{C}\) we have to pick \(\alpha_c\) to be the morphism \(F(c)\rightarrow G(c)\) and \(\alpha_{d}\) to be the morphism \(F(d)\rightarrow G(d)\).

  2. Counterexample:

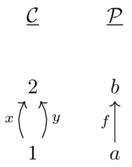
    • let \(F\) send \(f\mapsto x,a\mapsto1,b\mapsto 2\) and \(G\) maps everything to \(2\)

    • The naturality condition for f leaves us with two choices for \(\alpha_a\)

The category of instances on a schema(5)
Instance homomorphism(1)

An instance homomorphism between two database instances, \(\mathcal{C}\xrightarrow{I,J}\mathbf{Set}\)

Grph as functor category(1)

  • The category of graphs as a functor category

  • Schema for graphs: \(\mathbf{Gr}:=\boxed{\overset{Arr}\bullet \overset{src}{\underset{tar}{\rightrightarrows}}\overset{Vert}\bullet}\)

  • A graph instance has a set of points and a set of arrows, each of which has a source and target.

  • There is a bijection between graphs and Gr instances

  • The objects of GrInst are graphs, the morphisms are graph homomorphisms (natural transformations between two Gr to Set functors)

    • Each graph homomorphism contains two components, which are morphisms in Set:

      1. \(G(Vert) \xrightarrow{\alpha_{vert}} H(vert)\)

      2. \(G(Arr) \xrightarrow{\alpha_{arr}} H(Arr)\)

    • Naturality conditions

Arrow table(1)

  • Consider the graphs \(G:=\boxed{\overset{1}\bullet \xrightarrow{a} \overset{2}\bullet \xrightarrow{b}\overset{3}\bullet}\) and \(H:=\boxed{\overset{4}\bullet \overset{d}{\underset{c}{\rightrightarrows}}\overset{5}\bullet\circlearrowleft e}\)

  • The arrow table of their database instances are below:

  • G src tar
    a 1 2
    b 2 3

  • H src tar
    c 4 5
    d 4 5
    e 5 5

Linked by

Exercise 3-64(2)

Consider the graphs \(G,H\) from Example 3.63. We claim there is exactly one graph homomorphism such that \(\alpha_{Arr}(a)=d\). What is the other value of \(\alpha_{Arr}\), and what are the three values of \(\alpha_{Vert}\)?

Solution(1)

  • We need \(2 \mapsto 5\), so the source of \(\alpha_{Arr}(b)\) must be \(5\) (there is only one arrow to pick, \(e\)).

  • \(1 \mapsto 4,\ 2\mapsto 5,\ 3 \mapsto 5\)