Retraction(1)
It is possible for \(f;g=id\) but \(g;f \ne id\)
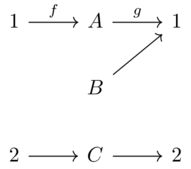
This is called a retraction rather than an isomorphism.
Isomorphisms formalize the notion of ‘interchangibility’, e.g. in a preorder the fact that \(a \cong b\) tells us that it doesn’t matter whether someone tells us \(c \leq a\) versus \(c \leq b\).
An isomorphism in a category
A morphism \(A \xrightarrow{f}B\) such that there exists a morphism \(B \xrightarrow{g}A\) satisfying \(f;g=id_A\) and \(g;f=id_B\)
We call f and g inverses and can write \(g=f^{-1}\)
We say A,B are isomorphic objects in this case.
The set \(\{a,b,c\}\) and \(\bar{3}\) are isomorphic (we have \(3!\) bijections to choose from). The isomorphisms in Set are the bijections.
It is possible for \(f;g=id\) but \(g;f \ne id\)

This is called a retraction rather than an isomorphism.
Show that the identity arrow on any given object is an isomorphism.
The inverse to \(id_c\) exists; it is itself: \(id_c ; id_c = id_c\) (from the identity property)
A monoid in which every morphism is an isomorphism is known as a group
Is the natural numbers monoid a group?
Is the monoid with the added constraint \(s;s=z\) a group?
No, \(s\) has no inverse (no natural number can be added to 1 to get 0)
Yes, this is the cyclic group with two elements.
Someone says that the only isomorphisms in \(\mathbf{Free}(G)\) for some graph \(G\) are the identity morphisms. Are they correct?
They are correct. If we could compose \(f;g\) to get a morphisms from c to c, a free category would pick a new morphism rather than re-use the identity (which could be forced with a constraint).