Functor pullback

The pullback of functor \(\mathcal{D}\xrightarrow{I}\mathbf{Set}\) along functor \(\mathcal{C}\xrightarrow{F}\mathcal{D}\)

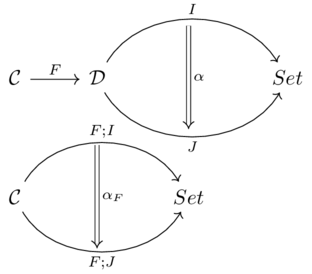
• The composite functor \(\mathcal{C}\xrightarrow{F;I}\mathbf{Set}\)

• Given a natural transformation \(I \overset{\alpha}\Rightarrow J\), there is a natural transformation \(\alpha_F\) whose components (morphisms in Set from \((F;I)(c)\) to \((F;J)(c)\), for any \(c \in \mathcal{C}\) are given by: \((\alpha_F)_c := \alpha_{F(c)}\)