Introducing wiring diagrams

Exercise 2-20(2)

Given the assertions the interior of this wiring diagram:
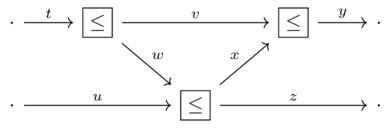
Prove that the conclusion follows using the rules of symmetric monoidal preorders
- Make sure to use reflexivity and transitivity
How do you know that symmetry axiom does not need to be invoked?

Solution(1)

Assertions:
- \(t \leq v+w\)
- \(w+u \leq x+z\)
- \(v+x \leq y\)
Conclusion: \(t+u \leq y+z\)
Proof:
- \((t)+(u) \leq (v+w)+(u)\) - from ?monotonicity and reflexivity of u
- \(= v+(w+u)\) - ?associativity
- \(\leq v+(x+z)\) - ?monotonicity and reflexivity of v
- \(= (v+x)+z\) - ?associativity
- \(\leq y+z\) - ?monotonicity and reflexivity of z
Symmetry was not needed because the diagram had no crossing wires.

Visual representations for building new relationships from old.

For a preorder without a monoidal structure, we can only chain relationships linearly (due to transitivity).

For a symmetric monoidal structure, we can combine relationships in series and in parallel.

Call boxes and wires icons

Any element \(x \in X\) can be a label for a wire. Given x and y, we can write them as two wires in parallel or one wire \(x \otimes y\); these are two ways of representing the same thing.

Consider a wire labeled \(I\) to be equivalent to the absence of a wire.

Given a \(\leq\) block, we say a wiring diagram is valid if the monoidal product of elements on the left is less than those on the right.

Let’s consider the properties of the order structure:

Reflexivity: a diagram consisting of just one wire is always valid.
Transitivity: diagrams can be connected together if outputs = inputs
Monotonicity: Stacking two valid boxes in parallel is still valid.
Unitality: We need not worry about \(I\) or blank space
Associativity: Need not worry about building diagrams from top-to-bottom or vice-versa.
Symmetry: A diaagram is valid even if its wires cross.

One may regard crossing wires as another icon in the iconography.

Wiring diagrams can be thought of as graphical proofs

If subdiagrams are true, then the outer diagram is true.