Symmetric monoidal preorders

Definition and first examples(9)

The notation for monoidal product and unit may vary depending on context. \(I, \otimes\) are defaults but it may be best to use \((0,+),(1,*),(true, \land)\) (etc.)

Symmetric monoidal structure on a preorder(1)

A symmetric monoidal structure on a preorder \((X, \leq)\)

  • Two additional constituents:

    1. A monoidal unit \(I \in X\)

    2. A monoidal product \(X \times X \xrightarrow{\otimes} X\)

  • Satisfying the following properties:

    1. Monotonicity: \(\forall x_1,x_2,y_1,y_2 \in X: x_1 \leq y_1 \land x_2 \leq y_2 \implies x_1 \otimes x_2 \leq y_1 \otimes y_2\)

    2. Unitality: \(\forall x \in X: I \otimes x = x = x \otimes I\)

    3. Associativity: \(\forall x,y,z \in X: (x \otimes y) \otimes z = x \otimes (y\otimes z)\)

    4. Symmetry: \(\forall x,y \in X: x \otimes y = y \otimes x\)

Linked by

Weak monoidal structure on a preorder(1)

A weak monoidal structure on a preorder \((X, \leq)\)

Definition is identical to a symmetric monoidal structure, replacing all \(=\) signs with \(\cong\) signs.

Discrete SMP(1)

  • A monoid is a set \(M\) with a monoid unit \(e \in M\) and associative monoid multiplication \(M \times M \xrightarrow{\star} M\) such that \(m \star e=m=e \star m\)

  • Every set \(S\) determines a discrete preorder: \(\mathbf{Disc}_S\)

  • It is easy to check if \((M,e,\star)\) is a commutative monoid then \((\mathbf{Disc}_M, =, e, \star)\) is a symmetric monoidal preorder.

Linked by

Poker hands(1)

  • Let \(H\) be the set of all poker hands, ordered by \(h \leq h'\) if \(h'\) beats or ties hand \(h\).

  • One can propose a monoidal product by assigning \(h_1 \otimes h_2\) to be “the best hand one can form out of the ten cards in \(h_1 \bigcup h_2\)"

  • This proposal will fail monotonicity with the following example:

    • \(h_1 := \{2\heartsuit, 3\heartsuit,10 \spadesuit,J\spadesuit,Q\spadesuit\} \leq i_1 := \{4\spadesuit,4\spadesuit,6\heartsuit,6\diamondsuit,10\diamondsuit\}\)

    • \(h_2 := \{2\diamondsuit,3\diamondsuit,4\diamondsuit,K\spadesuit,A\spadesuit\} \leq i_2 := \{5\spadesuit,5\heartsuit,7\heartsuit,J\diamondsuit,Q\diamondsuit\}\)

    • \(h_1 \otimes h_2=\{10\spadesuit,J\spadesuit,Q\spadesuit,K\spadesuit,A\spadesuit\} \not \leq i_2 \otimes i_2 = \{5\spadesuit, 5\heartsuit,6\heartsuit,6\diamondsuit,Q\diamondsuit\}\)

Exercise 2-5(2)

Consider the reals ordered by our normal \(\leq\) relation. Do \((1,*)\) as unit and product for a symmetric monoidal structure?

Solution(1)

No, monotonicity fails: \(x_1\leq y_1 \land x_2 \leq y_2 \not \implies x_1x_2 \leq y_1y_2\) (Counterexample: \(x_1=x_2=-1, y_1=y_2=0\))

Exercise 2-8(2)

Check if \((M,e,\star)\) is a commutative monoid then \((\mathbf{Disc}_M, =, e, \star)\) is a symmetric monoidal preorder, as described in this example.

Solution(1)

  • Monotonicity is the only tricky one, and is addressed due to the triviality of the discrete preorder.

    • We can replace \(x \leq y\) with \(x \leq x\) because it is a discrete preorder.

    • \(x_1 \leq x_1 \land x_2 \leq x_2 \implies x_1 \otimes x_2 \leq x_1 \otimes x_2\)

    • \(True \land True \implies True\) is vacuously true due to reflexivity of preorder.

  • Unitality/associativity comes from unitality/associativity of monoid

  • Symmetry comes from commutitivity of monoid.

Introducing wiring diagrams(3)
Exercise 2-20(2)

  • Given the assertions the interior of this wiring diagram:

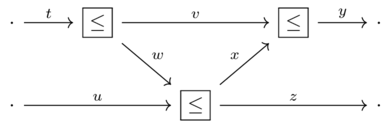
  • Prove that the conclusion follows using the rules of symmetric monoidal preorders

    • Make sure to use reflexivity and transitivity

  • How do you know that symmetry axiom does not need to be invoked?

Solution(1)

  • Assertions:

    • \(t \leq v+w\)

    • \(w+u \leq x+z\)

    • \(v+x \leq y\)

  • Conclusion: \(t+u \leq y+z\)

  • Proof:

    • \((t)+(u) \leq (v+w)+(u)\) - from monotonicity and reflexivity of u

    • \(= v+(w+u)\) - associativity

    • \(\leq v+(x+z)\) - monotonicity and reflexivity of v

    • \(= (v+x)+z\) - associativity

    • \(\leq y+z\) - monotonicity and reflexivity of z

  • Symmetry was not needed because the diagram had no crossing wires.

Applied examples(1)
Abstract examples(18)
Opposite SMP(2)

The opposite of a symmetric monoidal preorder \((X, \geq, I, \otimes)\) is still a symmetric monoidal preorder

Proof(1)

  • Monotonicity: \(x_1 \geq y_1 \land x_2 \geq y_2 \implies x_1 \otimes x_2 \geq y_1 \otimes y_2\)

    • This holds because monotonicity holds in the original preorder (\(a\geq b \equiv b \leq a\)).

  • Unitality, symmetry, and associativity are not affected by the preorder.

Natural numbers SMP(1)

There is a symmetric monoidal structure on \((\mathbb{N}, \leq)\) where the monoidal unit is zero and the product is \(+\) (\(6+4=10\)). Monotonicity (\((x_1,x_2)\leq(y_1,y_2) \implies x_1+x_2 \leq y_1+y_2\)) and other conditions hold.

Divisibility SMP(1)

  • Recall the divisibility order \((\mathbb{N}, |)\)

  • There is a symmetric monoidal structure on this preorder with unit \(1\) and product \(*\).

  • Monotonicity (\(x_1|y_1 \land x_2|y_2 \implies x_1*x_2 | y_1*y_2\)) and other conditions hold.

Cost SMP(1)

  • Lawvere’s symmetric monoidal preorder, Cost.

  • Let \([0,\infty]\) represent the non-negative real numbers with infinity. Also take the usual notion of \(\geq\).

  • There is a monoidal structure for this preorder: \(\mathbf{Cost}:=([0,\infty],\geq,0,+)\)

    • The monoidal unit being zero means “you can get from a to a at no cost."

    • The product being + means “getting from a to c is at most the cost of a to b plus b to c"

    • The ‘at most’ above comes from the \(\geq\).

Linked by

Exercise 2-31(2)

Show there is a symmetric monoidal structure on \((\mathbb{N}, \leq)\) where the monoidal product is \(6*4=24\). What should the monoidal unit be?

Solution(1)

  • Let the monoidal product be the standard product for integers, with 1 as unit.

    • Monotonicity: \((x_1,x_2)\leq (y_1,y_2) \implies x_1x_2 \leq y_1y_2\)

    • Unitality: \(1*x_1=x_1=x_1*1\)

    • Associativity: \(a*(b*c)=(a*b)*c\)

    • Symmetry: \(a*b=b*a\)

Exercise 2-33(2)

Recall the divisibility order \((\mathbb{N}, |)\). Someone proposes \((0,+)\) as the monoidal unit and product. Does this satisfy the conditions of a symmetric monoidal structure?

Solution(1)

Conditions 2-4 are satisfied, but not monotonicity: \(1|1 \land 2|4\) but not \(3 | 5\)

Exercise 2-34(2)

  • Consider the preorder defined by the Hasse diagram \(\boxed{no \rightarrow maybe \rightarrow yes}\)

  • Consider a potential monoidal structure with \(yes\) as the unit and \(min\) as the product.

  • Fill out a reasonable definition of \(min\) and check that it satisfies the conditions.

Solution(1)
\(min\) no maybe yes
no no no no
maybe no maybe maybe
yes no maybe yes

  • Monotonicity: \(x_1 \leq y_1 \land x_2 \leq y_2 \implies x_1x_2 \leq y_1y_2\)

    • Suppose without loss of generality that \(x_1\leq x_2\)

    • then \(x_1x_2=x_1\) and \(y_1y_2 = y_1\) or \(y_2\)

    • In the first case, we know this is true because we assumed \(x_1 \leq y_1\)

    • In the second case, we know it from transitivity: \(x_1 \leq x_2\leq y_2\)

  • Unitality: \(min(x,yes)=x\)

  • Associativity: probably

  • Symmetry: table is symmetric.

Linked by

Exercise 2-35(2)

Check that there is a symmetric monoidal structure on the power set of \(S\) ordered by subset relation. (The unit is \(S\) and product is \(\cap\))

Solution(1)

  • Monotonicity: \(x_1 \subseteq y_1 \land x_2 \subseteq y_2 \implies x_1 \cap x_2 \subseteq y_1 \cap y_2\)

    • This is true: if something is in both \(x_1,x_2\), then it is in both \(y_1,y_2\), i.e. in their intersection.

  • Unitality: \(x \cap S = x = S \cap x\), since \(\forall x \in P(S): x \subseteq S\).

  • Associativity and symmetry come from associativity and symmetry of \(\cap\) operator.

Exercise 2-36(2)

  • Let \(Prop^\mathbb{N}\) be the set of all mathematical statements one can make about a natural number.

  • Examples:

    • n is a prime

    • n = 2

    • \(n \geq 11\)

  • We say \(P \leq Q\) if for all \(n \in \mathbb{N}\), \(P(n) \implies Q(n)\)

  • Define a monoidal unit and product on \((Prop^\mathbb{N}, \leq)\).

Solution(1)

  • Let the unit be \(\lambda x. true\) and product be \(\land\)

  • montonicity: \(P_1(x)\leq Q_1(x) \land P_2(x) \leq Q_2(x) \implies (P_1 \land P_2)(x) \leq (Q_1 \land Q_2)(x)\)

    • If the \(P\) properties hold for a given number, then each of the \(Q\) properties hold

  • unitality, associativity, symmetry: same as \(\mathbf{Bool}\)

Exercise 2-40(2)

Consider \(\mathbf{Cost}^{op}\). What is it as a preorder? What is its unit and product?

Solution(1)

As a preorder, the domain is still \([0,\infty]\) and ordered by the natural \(\leq\) relation. The unit and product are unchanged by taking the opposite preorder, so they are still \(0, +\) respectively.

Monoidal monotone maps(9)

Monoidal montones are examples of monoidal functors, specifically lax ones. Oplax functors are a dual notion which has the inequalities reversed.

Monoidal monotone(1)

A monoidal monotone map from \((P,\leq_P,I_P,\otimes_P)\) to \((Q, \leq_Q,I_Q,\otimes_Q)\). Also, a strong monoidal monotone map and a strict monoidal monotone map

  • A monotone map \((P,\leq_P) \xrightarrow{f} (Q,\leq_Q)\) satsifying two conditions:

    1. \(I_Q \leq_Q f(I_P)\)

    2. \(\forall p_1,p_2 \in P:\) \(f(p_1)\ \otimes_Q\ f(p_2)\ \leq_Q\ f(p_1\ \otimes_P\ p_2)\)

  • If the \(\leq\) are replaced with \(\cong\), the map is strong, and if replaced with \(=\), it is strict.

Linked by

Natural Real monoidal monotones(1)

  • Strict monoidal monotone injection \((\mathbb{N},\leq, 0, +) \xhookrightarrow{i} (\mathbb{R},\leq,0,+)\)

  • There is also a monoidal monotone \((\mathbb{R}^+,\leq, 0, +) \xrightarrow{\lfloor x \rfloor} (\mathbb{N},\leq,0,+)\)

    • Monotonic: \(x \leq_\mathbb{R} y \implies \lfloor x \rfloor \leq \lfloor y \rfloor\)

    • But it is neither strict nor strong: \(\lfloor 0.5 \rfloor + \lfloor 0.5 \rfloor \not \cong \lfloor 0.5+0.5 \rfloor\)

Exercise 2-43(2)

Consider a proposed monoidal monotone \(\mathbf{Bool}\xrightarrow{g}\mathbf{Cost}\) with \(g(false)=\infty, g(true)=0\)

  • Check that the map is monotonic and that it satisfies both properties of monoidal monotones.

  • Is g strict?

Solution(1)

  • It is monotonic: \(\forall a,b \in \mathbb{B}: a\leq b \implies g(a)\leq g(b)\)

    • there is only one nonidentity case in \(\mathbf{Bool}\) to cover, and it is true that \(\infty\ \leq_\mathbf{Cost}\ 0\).

  • Condition on units: \(0 \leq_\mathbf{Cost} g(true)\) (actually, it is equal)

  • In \(\mathbf{Cost}\): \(g(x) + g(y) \geq g(x \land y)\)

    • if both true/false, the equality condition holds.

    • If one is true and one is false, then LHS and RHS are \(\infty\) (as \(x \land y = False\)).

  • Therefore this is a strict monoidal monotone.

Exercise 2-44(2)

  • Consider the following functions \(\mathbf{Cost} \xrightarrow{d,u} \mathbf{Bool}\)

    • \(d(x>0)\mapsto false,\ d(0)\mapsto true\)

    • \(u(x=\infty)\mapsto false,\ d(x < \infty) \mapsto true\)

  • For both of these, answer:

    1. Is it monotonic?

    2. If so, does it satsify the monoidal monotone properties?

    3. If so, is it strict?

Solution(1)

  • The function \(d\) asks “Is it zero?”, and the function \(u\) asks “Is it finite?”.

  • Both of these questions are monotone: as we traverse forward in \(\leq_{Cost}\), we traverse towards being zero or being finite.

  • The first monoidal monotone axiom is satisifed in both because the unit (\(0\)) is mapped to the unit (\(True\)).

  • The second monoidal monotone axiom holds for both because addition preserves both things being zero (or not) and both things being finite (or not).

  • These are strict because, in \(Bool\), equality and congruence coincide.

Linked by

Exercise 2-45(2)

  1. Is \((\mathbb{N},\leq,1,*)\) a symmetric monoidal preorder?

  2. If so, does there exist a monoidal monotone \((\mathbb{N},\leq,0,+) \rightarrow (\mathbb{N},\leq,1,*)\)

  3. Is \((\mathbb{Z},\leq,*,1)\) a symmetric monoidal preorder?

Solution(1)

  1. Yes. Monotonicity holds, and multiplication by 1 is unital. The operator is symmetric and associative.

  2. Exponentiation (say, by \(2\)) is a strict monoidal monotone.

    • \(1 = 2^0\) and \(2^x * 2^y = 2^{x+y}\)

  3. No: monotonicity does not hold (multiplying negative numbers gives a larger number).