Exercise 2-63

Consider the symmetric monoidal preorder \(\mathcal{W}:=(\mathbb{N}\cup\{\infty\},\leq,\infty,min)\)

  1. Draw a small graph labeled by elements of \(\mathbb{N}\cup\{\infty\}\)

  2. Write a the matrix whose rows and columns are indexed by nodes in the graph, whose (x,y)th entry is given by the maximum over all paths p from x to y of the minimum edge label in p.

  3. Prove that this matrix is a matrix of hom-objects for a \(\mathcal{W}\) category called \(\mathcal{X}\).

  4. Make up an interpretation for what it means to enrich in \(\mathcal{W}\)

Solution(1)

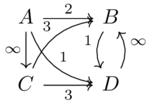
  1. (implicitly, no path means path of weight 0, and self paths have weight \(\infty\))

  2. Maxmin matrix:

    A B C D
    A \(\infty\) 3 \(\infty\) 3
    B 0 \(\infty\) 0 \(\infty\)
    C 0 3 \(\infty\) 3
    D 0 1 0 \(\infty\)

    Self paths are equal to the monoidal unit and it will never be the case that \(min(\mathcal{X}(A,B),\mathcal{X}(B,C)) > \mathcal{X}(A,C)\) because even in the worst-case scenario (where there is not a better path from A to C that ignores B completely), we form the best path by combining the best path from A to B with the best from B to C. We are forced to take the minimum edge label in the path, which means that the lowest \(\mathcal{X}(A,C)\) can be is actually equal to the left hand side.

  3. The edges could represent constraints (\(\infty\) is fully unconstrained, \(0\) is fully constrained, e.g. the diameter of a pipe) and the hom-object represents the least-constrained thing that can get from one point to another. The monoidal unit says that something can be fully unconstrained if it stays where it is, and the monoidal product (min) says how to compose two different constraints in series.