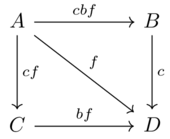
(implicitly, no path means edge of \(\varnothing\) and self paths are \(cfb\))
Hom objects:
| A | B | C | D | |
|---|---|---|---|---|
| A | cbf | cbf | cf | cf |
| B | \(\varnothing\) | cbf | \(\varnothing\) | c |
| C | \(\varnothing\) | \(\varnothing\) | cbf | bf |
| D | \(\varnothing\) | \(\varnothing\) | \(\varnothing\) | cbf |
The first property (\(\forall x \in Ob(\mathcal{X}): I \leq \mathcal{X}(x,x)\)) is satisfied by noting the diagonal entries are equal to the unit.
The second property (\(\forall x,y,z \in Ob(\mathcal{X}): \mathcal{X}(x,y)\otimes\mathcal{X}(y,z) \leq \mathcal{X}(x,z)\)) can be checked looking at the following cases:
\(A \rightarrow B \rightarrow D\): \(cbf \cap c \leq cf\)
\(A \rightarrow C \rightarrow D\): \(cf \cap bf \leq cf\)
One subtlety is that we need to say that one can get from any place to itself by any means of transportation for this to make sense. Overall interpretation looks good.