Exercise 2-62

Let \(M\) be a set and \(\mathcal{M}:=(P(M),\subseteq, M, \cap)\) be the symmetric monoidal preorder whose elements are subsets of \(M\).

Someone says "for any set \(M\), imagine it as the set of modes of transportation (e.g. car, boat, foot)". Then an \(\mathcal{M}\) category \(\mathcal{X}\) tells you all the modes that will get you from a all the way to b, for any two points \(a,b \in Ob(\mathcal{X})\)

Draw a graph with four vertices and five edges, labeled with a subset of \(M=\{car,boat,foot\}\)
From this graph it is possible to construct an \(\mathcal{M}\) category where the hom-object from x to y is the union of the sets for each path from x to y, where the set of a path is the intersection of the sets along the path. Write out the corresponding 4x4 matrix of hom-objects and convince yourself this is indeed an \(\mathcal{M}\) category.
Does the person’s interpretation look right?

Solution(1)

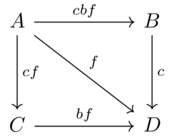
(implicitly, no path means edge of \(\varnothing\) and self paths are \(cfb\))
Hom objects:?

A B C D

A cbf cbf cf cf

B \(\varnothing\) cbf \(\varnothing\) c

C \(\varnothing\) \(\varnothing\) cbf bf

D \(\varnothing\) \(\varnothing\) \(\varnothing\) cbf
- The first property (\(\forall x \in Ob(\mathcal{X}): I \leq \mathcal{X}(x,x)\)) is satisfied by noting ?the diagonal entries are equal to the unit.
- The second property (\(\forall x,y,z \in Ob(\mathcal{X}): \mathcal{X}(x,y)\otimes\mathcal{X}(y,z) \leq \mathcal{X}(x,z)\)) can be checked looking at the following cases:?
  - \(A \rightarrow B \rightarrow D\): \(cbf \cap c \leq cf\)
  - \(A \rightarrow C \rightarrow D\): \(cf \cap bf \leq cf\)
One subtlety is that we need to say that one can get from any place to itself by any means of transportation for this to make sense. Overall interpretation looks good.

	A	B	C	D
A	cbf	cbf	cf	cf
B	\(\varnothing\)	cbf	\(\varnothing\)	c
C	\(\varnothing\)	\(\varnothing\)	cbf	bf
D	\(\varnothing\)	\(\varnothing\)	\(\varnothing\)	cbf