V-variations on preorders and metric spaces

Exercise 2-61(2)

Recall the symmetric monoidal preorder \(\mathbf{NMY} := (P,\leq, yes, min)\) from Exercise 2.34. Interpret what a NMY-category is.

Solution(1)

It is like a graph where some edges are ‘maybe’ edges. We can ask the question “Is there a path from a to b?" and if there is a true path we will get a ‘yes’. If the only paths are those which include maybe edges, then we get a ’maybe’. If there’s no path at all, we get a ‘no’.

Exercise 2-62(2)

Let \(M\) be a set and \(\mathcal{M}:=(P(M),\subseteq, M, \cap)\) be the symmetric monoidal preorder whose elements are subsets of \(M\).
Someone says "for any set \(M\), imagine it as the set of modes of transportation (e.g. car, boat, foot)". Then an \(\mathcal{M}\) category \(\mathcal{X}\) tells you all the modes that will get you from a all the way to b, for any two points \(a,b \in Ob(\mathcal{X})\)
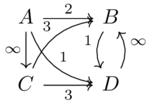
1. Draw a graph with four vertices and five edges, labeled with a subset of \(M=\{car,boat,foot\}\)
2. From this graph it is possible to construct an \(\mathcal{M}\) category where the hom-object from x to y is the union of the sets for each path from x to y, where the set of a path is the intersection of the sets along the path. Write out the corresponding 4x4 matrix of hom-objects and convince yourself this is indeed an \(\mathcal{M}\) category.
3. Does the person’s interpretation look right?

Solution(1)

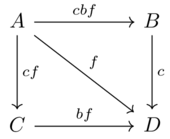
(implicitly, no path means edge of \(\varnothing\) and self paths are \(cfb\))
Hom objects:?

A B C D

A cbf cbf cf cf

B \(\varnothing\) cbf \(\varnothing\) c

C \(\varnothing\) \(\varnothing\) cbf bf

D \(\varnothing\) \(\varnothing\) \(\varnothing\) cbf
- The first property (\(\forall x \in Ob(\mathcal{X}): I \leq \mathcal{X}(x,x)\)) is satisfied by noting ?the diagonal entries are equal to the unit.
- The second property (\(\forall x,y,z \in Ob(\mathcal{X}): \mathcal{X}(x,y)\otimes\mathcal{X}(y,z) \leq \mathcal{X}(x,z)\)) can be checked looking at the following cases:?
  - \(A \rightarrow B \rightarrow D\): \(cbf \cap c \leq cf\)
  - \(A \rightarrow C \rightarrow D\): \(cf \cap bf \leq cf\)
One subtlety is that we need to say that one can get from any place to itself by any means of transportation for this to make sense. Overall interpretation looks good.

	A	B	C	D
A	cbf	cbf	cf	cf
B	\(\varnothing\)	cbf	\(\varnothing\)	c
C	\(\varnothing\)	\(\varnothing\)	cbf	bf
D	\(\varnothing\)	\(\varnothing\)	\(\varnothing\)	cbf

Exercise 2-63(2)

Consider the symmetric monoidal preorder \(\mathcal{W}:=(\mathbb{N}\cup\{\infty\},\leq,\infty,min)\)

Draw a small graph labeled by elements of \(\mathbb{N}\cup\{\infty\}\)
Write a the matrix whose rows and columns are indexed by nodes in the graph, whose (x,y)th entry is given by the maximum over all paths p from x to y of the minimum edge label in p.
Prove that this matrix is a matrix of hom-objects for a \(\mathcal{W}\) category called \(\mathcal{X}\).
Make up an interpretation for what it means to enrich in \(\mathcal{W}\)

Solution(1)

(implicitly, no path means path of weight 0, and self paths have weight \(\infty\))
Maxmin matrix:

A B C D

A \(\infty\) 3 \(\infty\) 3

B 0 \(\infty\) 0 \(\infty\)

C 0 3 \(\infty\) 3

D 0 1 0 \(\infty\)

Self paths are equal to ?the monoidal unit and it will never be the case that \(min(\mathcal{X}(A,B),\mathcal{X}(B,C)) > \mathcal{X}(A,C)\) because even in the worst-case scenario (where there is not a better path from A to C that ignores B completely), we form the best path by ?combining the best path from A to B with the best from B to C. We are forced to take the minimum edge label in the path, which means that the lowest \(\mathcal{X}(A,C)\) can be is actually equal to the left hand side.
The edges could represent ?constraints (\(\infty\) is fully unconstrained, \(0\) is fully constrained, e.g. the diameter of a pipe) and the hom-object represents the ?least-constrained thing that can get from one point to another. The monoidal unit says that ?something can be fully unconstrained if it stays where it is, and the monoidal product (min) says ?how to compose two different constraints in series.

	A	B	C	D
A	\(\infty\)	3	\(\infty\)	3
B	0	\(\infty\)	0	\(\infty\)
C	0	3	\(\infty\)	3
D	0	1	0	\(\infty\)