Product V-categories

The \(\mathcal{V}\) product of two \(\mathcal{V}\) categories, \(\mathcal{X} \times \mathcal{Y}\)

This is also a \(\mathcal{V}\) category with:

1. \(Ob(\mathcal{X}\times\mathcal{Y}) := Ob(\mathcal{X})\times Ob(\mathcal{Y})\)

2. \((\mathcal{X} \times \mathcal{Y})((x,y),(x',y')) := \mathcal{X}(x,x') \otimes \mathcal{Y}(y,y')\)

Linked by

• Solution: referenced

• Let \(\mathcal{X}\) and \(\mathcal{Y}\) be the Lawvere metric spaces (i.e. Costcategories) defined by the following weighted graphs.

• 

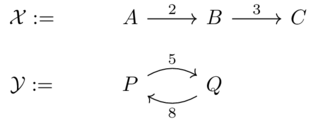
• The product can be represented by the following graph: ?

  

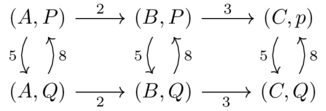
• The distance between any two points \((x,y),(x',y')\) is given by ?the sum \(d_X(x,x)+d_Y(y,y)\).

• We can also consider the Cost-categories as matrices

  \(\mathcal{X}\)	A	B	C
  A	0	2	5
  B	\(\infty\)	0	3
  C	\(\infty\)	\(\infty\)	0

  \(\mathcal{Y}\)	P	Q
  P	0	5
  Q	8	0

  \(\mathcal{X}\times\mathcal{Y}\)	(A,P)	(B,P)	(C,P)	(A,Q)	(B,Q)	(C,Q)
  (A,P)	0	2	5	5	7	10
  (B,P)	\(\infty\)	0	3	\(\infty\)	5	8
  (C,P)	\(\infty\)	\(\infty\)	0	\(\infty\)	\(\infty\)	5
  (A,Q)	8	10	13	0	2	5
  (B,Q)	\(\infty\)	8	11	\(\infty\)	0	3
  (C,Q)	\(\infty\)	\(\infty\)	8	\(\infty\)	\(\infty\)	0

• Can view this as a 2x2 grid of 3x3 blocks: each is ?a \(\mathcal{X}\) matrix shifted by \(\mathcal{Y}\).

Let \(\mathcal{X} \times \mathcal{Y}\) be the \(\mathcal{V}\)-product of two \(\mathcal{V}\) categories.

1. Check that for every object we have \(I \leq (\mathcal{X} \times \mathcal{Y})((x,y),(x,y))\)

2. Check that for every three objects we have:

   • \((\mathcal{X} \times \mathcal{Y})((x_1,y_1),(x_2,y_2)) \otimes (\mathcal{X} \times \mathcal{Y})((x_2,y_2),(x_3,y_3)) \leq (\mathcal{X} \times \mathcal{Y})((x_1,y_1),(x_3,y_3))\)

Solution(1)

1. • By axioms of \(\mathcal{V}\) categories: \(I \leq \mathcal{X}(x,x')=xx\) and \(I \leq \mathcal{Y}(y,y')=yy\)

   • ?By monotonicity: \(I \leq xx \land I \leq yy\) implies \(I = I \otimes I \leq xx \otimes yy\).

   • By the definition of a product category this last term can be written as \((\mathcal{X} \times \mathcal{Y})((x,y),(x,y))\)

2. • By axioms of \(\mathcal{V}\) categories: \(\mathcal{X}(x_1,x_2) \otimes \mathcal{X}(x_2,x_3) \leq \mathcal{X}(x_1,x_3)\) and \(\mathcal{Y}(y_1,y_2) \otimes \mathcal{Y}(y_2,y_3) \leq \mathcal{Y}(y_1,y_3)\)

   • ?Therefore, by monotonicity, we have \((\mathcal{X}(x_1,x_2) \otimes \mathcal{X}(x_2,x_3)) \otimes (\mathcal{Y}(y_1,y_2) \otimes \mathcal{Y}(y_2,y_3)) \leq \mathcal{X}(x_1,x_3) \otimes \mathcal{Y}(y_1,y_3)\)

   • Desugaring the definiton of the hom-object in \(\mathcal{X}\times\mathcal{Y}\), the property we need to show is that \((\mathcal{X}(x_1,x_2) \otimes\mathcal{Y}(y_1,y_2)) \otimes (\mathcal{X}(x_2,x_3) \otimes\mathcal{Y}(y_2,y_3)) \leq (\mathcal{X}(x_1,x_3) \otimes\mathcal{Y}(y_1,y_3))\)

   • Given ?the associativity and commutitivity of the \(\otimes\) operator, we can rearange the order and ignore parentheses for the four terms on the LHS. Do this to yield the desired expression.

• Consider \(\mathbb{R}\) as a Lawvere metric space, i.e. as a Cost-category.

• Form the Cost-product \(\mathbb{R}\times\mathbb{R}\).

• What is the distance from \((5,6)\) to \((-1,4)\)?

Solution(1)

The distance is the Manhattan/\(L_1\) distance: \(|5-(-1)| + |6-4| = 8\)