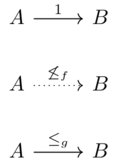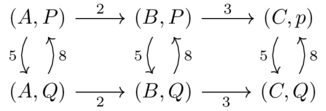Constructions on V-categories

Changing the base of enrichment(7)
Induced V-categories from monoidal monotones(2)

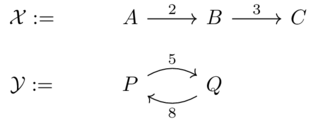
Let \(\mathcal{V}\xrightarrow{f}\mathcal{W}\) be a monoidal monotone map. Given a \(\mathcal{V}\) category, called \(\mathcal{C}\), one can construct an associated \(\mathcal{W}\) category, let’s call it \(\mathcal{C}_f\)

Proof(1)

  • Take the same objects: \(Ob(\mathcal{C}_f):=Ob(\mathcal{C})\)

  • \(\mathcal{C}_f(a,b) := f(\mathcal{C}(a,b))\)

  • Check this obeys the definition of an enriched category:

    • Condition on the monoidal unit:

      1. \(I_W \leq f(I_V)\) — from the first condition of a monoidal monotone map.

      2. \(\forall c \in Ob(\mathcal{C}): I_V \leq \mathcal{C}(c,c)\) — first condition of an enriched category, which \(\mathcal{C}\) is

      3. \(\forall c \in Ob(\mathcal{C}):f(I_V) \leq f(\mathcal{C}(c,c))\) — monotone map property

      4. \(\forall c \in Ob(\mathcal{C}):f(I_V) \leq \mathcal{C}_f(c,c)\) — definition of \(\mathcal{C}_f\)

      5. \(\forall c \in Ob(C_f): I_W \leq C_f(c,c)\) — transitivity, using 1 and 4, noting \(Ob(\mathcal{C})=Ob(\mathcal{C}_f)\)

    • Condition on monoidal product:

      1. \(\mathcal{C}_f(c,d) \otimes_W \mathcal{C}_f(d,e) = f(\mathcal{C}(c,d)) \otimes_W f(\mathcal{C}(d,e))\) — definition of \(\mathcal{C}_f\)

      2. \(f(\mathcal{C}(c,d)) \otimes_W f(\mathcal{C}(d,e)) \leq f(\mathcal{C}(c,d) \otimes_V \mathcal{C}(d,e))\) — second condition of a monoidal monotone map

      3. \(\mathcal{C}(c,d) \otimes_V \mathcal{C}(d,e) \leq \mathcal{C}(c,e)\) — Second condition of an enriched category

      4. \(f(\mathcal{C}(c,d) \otimes_V \mathcal{C}(d,e)) \leq f(\mathcal{C}(c,e)\) — monotone map property

      5. \(f(\mathcal{C}(c,d) \otimes_V \mathcal{C}(d,e)) \leq \mathcal{C}_f(c,e)\) — definition of \(\mathcal{C}_f\)

      6. \(\mathcal{C}_f(c,d) \otimes_W \mathcal{C}_f(d,e) \leq \mathcal{C}_f(c,e)\) — transitivity, 1,2 and 5

Linked by

Metric space to preorder(1)

  • Consider the function \([0,\infty] \xrightarrow{f} \mathbb{B}\) which maps 0 to true and otherwise to false.

  • Can check that f is monotonic and preserves the monoidal product+unit, so it is a monoidal monotone. (this was shown in Exercise 2.44)

  • Thus we have a tool to convert metric spaces into preorders.

Linked by

Exercise 2-67(2)

Recall the “regions of the world” Hausdorff metric space We learned that a metric space can be converted into a preorder by a particular monoidal monotone map. How would you interpret the resulting preorder?

Solution(1)

The edges in the preorder represent the \(\subseteq\) relation. For Boston, US, and Spain, it would look like this (with implicit self-edges):

Exercise 2-68(2)

Find a different monoidal monotone map \(\mathbf{Cost}\xrightarrow{g}\mathbf{Bool}\) from the one in Example 2.65. Using the construction from Proposition 2.64, convert a Lawvere metric space into two different preorders. Find a metric space for which this happens.NOCARD

Solution(1)
Enriched functors(5)
V-functor(1)

A \(\mathcal{V}\) functor \(\mathcal{X}\xrightarrow{F}\mathcal{Y}\) between two \(\mathcal{V}\) categories

A function \(Ob(\mathcal{X})\xrightarrow{F}Ob(\mathcal{Y})\) subject to the constraint:

  • \(\forall x_1,x_2 \in Ob(\mathcal{X}): \mathcal{X}(x_1,x_2) \leq \mathcal{Y}(F(x_1),F(x_2))\)

Linked by

Bool-functors(1)

  • Monotone maps, considering the source and target preorders as Bool-categories, are in fact Bool-functors.

  • The monotone map constraint, that \(x_1\ \leq_X\ x_2 \implies F(x_1)\leq_Y F(x_2)\), translates to the enriched category functor constraint, that \(\mathcal{X}(x_1,x_2) \leq \mathcal{Y}(F(x_1),F(x_2))\).

Cost-functors(1)

  • A Cost-functor is also known as a Lipschitz function.

  • Therefore a Lipschitz function is one under which the distance between any pair of points does not increase.

Exercise 2-73(2)

  • The concepts of opposite/dagger/skeleton extend from preorders to \(\mathcal{V}\) categories.

    • An opposite \(\mathcal{V}\) category \(\mathcal{X}\) has the same objects and \(\mathcal{X}^{op}(x,y):=\mathcal{X}(y,x)\)

    • A dagger category is identical to its opposite.

    • A skeletal \(\mathcal{V}\) category is one in which \(I \leq \mathcal{X}(x,y) \land I \leq \mathcal{X}(y,x)\) implies \(x = y\)

  • Recall an extended metric space \((X,d)\) is a Lawvere metric space with two extra properties.

  • Show that a skeletal dagger Cost-category is an extended metric space

Solution(1)

  • The skeletal dagger cost category has a set of objects, \(Ob(\mathcal{X})\) which we can call points.

  • For any pair of points, we assign a hom-object in \([0,\infty]\) (we can call this a distance function).

  • Skeletal property enforces the constraint \(d(x,y)=0 \iff x=y\).

  • The second enriched category property enforces the triangle inequality.

  • Because we have a dagger category, our distance function is forced to be symmetric.

  • Just like the information of a preorder is discarded (to yield a set) when we only consider skeletal dagger preorders, information must be discarded from Cost-categories to yield a Lawvere metric space.

Linked by

Product V-categories(6)
V-category product(1)

The \(\mathcal{V}\) product of two \(\mathcal{V}\) categories, \(\mathcal{X} \times \mathcal{Y}\)

This is also a \(\mathcal{V}\) category with:

  1. \(Ob(\mathcal{X}\times\mathcal{Y}) := Ob(\mathcal{X})\times Ob(\mathcal{Y})\)

  2. \((\mathcal{X} \times \mathcal{Y})((x,y),(x',y')) := \mathcal{X}(x,x') \otimes \mathcal{Y}(y,y')\)

Linked by

Cost-category product(1)

  • Let \(\mathcal{X}\) and \(\mathcal{Y}\) be the Lawvere metric spaces (i.e. Costcategories) defined by the following weighted graphs.

  • The product can be represented by the following graph:

  • The distance between any two points \((x,y),(x',y')\) is given by the sum \(d_X(x,x)+d_Y(y,y)\).

  • We can also consider the Cost-categories as matrices

    \(\mathcal{X}\) A B C
    A 0 2 5
    B \(\infty\) 0 3
    C \(\infty\) \(\infty\) 0
    \(\mathcal{Y}\) P Q
    P 0 5
    Q 8 0
    \(\mathcal{X}\times\mathcal{Y}\) (A,P) (B,P) (C,P) (A,Q) (B,Q) (C,Q)
    (A,P) 0 2 5 5 7 10
    (B,P) \(\infty\) 0 3 \(\infty\) 5 8
    (C,P) \(\infty\) \(\infty\) 0 \(\infty\) \(\infty\) 5
    (A,Q) 8 10 13 0 2 5
    (B,Q) \(\infty\) 8 11 \(\infty\) 0 3
    (C,Q) \(\infty\) \(\infty\) 8 \(\infty\) \(\infty\) 0

  • Can view this as a 2x2 grid of 3x3 blocks: each is a \(\mathcal{X}\) matrix shifted by \(\mathcal{Y}\).

Exercise 2-75(2)

Let \(\mathcal{X} \times \mathcal{Y}\) be the \(\mathcal{V}\)-product of two \(\mathcal{V}\) categories.

  1. Check that for every object we have \(I \leq (\mathcal{X} \times \mathcal{Y})((x,y),(x,y))\)

  2. Check that for every three objects we have:

    • \((\mathcal{X} \times \mathcal{Y})((x_1,y_1),(x_2,y_2)) \otimes (\mathcal{X} \times \mathcal{Y})((x_2,y_2),(x_3,y_3)) \leq (\mathcal{X} \times \mathcal{Y})((x_1,y_1),(x_3,y_3))\)

Solution(1)

    • By axioms of \(\mathcal{V}\) categories: \(I \leq \mathcal{X}(x,x')=xx\) and \(I \leq \mathcal{Y}(y,y')=yy\)

    • By monotonicity: \(I \leq xx \land I \leq yy\) implies \(I = I \otimes I \leq xx \otimes yy\).

    • By the definition of a product category this last term can be written as \((\mathcal{X} \times \mathcal{Y})((x,y),(x,y))\)

    • By axioms of \(\mathcal{V}\) categories: \(\mathcal{X}(x_1,x_2) \otimes \mathcal{X}(x_2,x_3) \leq \mathcal{X}(x_1,x_3)\) and \(\mathcal{Y}(y_1,y_2) \otimes \mathcal{Y}(y_2,y_3) \leq \mathcal{Y}(y_1,y_3)\)

    • Therefore, by monotonicity, we have \((\mathcal{X}(x_1,x_2) \otimes \mathcal{X}(x_2,x_3)) \otimes (\mathcal{Y}(y_1,y_2) \otimes \mathcal{Y}(y_2,y_3)) \leq \mathcal{X}(x_1,x_3) \otimes \mathcal{Y}(y_1,y_3)\)

    • Desugaring the definiton of the hom-object in \(\mathcal{X}\times\mathcal{Y}\), the property we need to show is that \((\mathcal{X}(x_1,x_2) \otimes\mathcal{Y}(y_1,y_2)) \otimes (\mathcal{X}(x_2,x_3) \otimes\mathcal{Y}(y_2,y_3)) \leq (\mathcal{X}(x_1,x_3) \otimes\mathcal{Y}(y_1,y_3))\)

    • Given the associativity and commutitivity of the \(\otimes\) operator, we can rearange the order and ignore parentheses for the four terms on the LHS. Do this to yield the desired expression.

Exercise 2-78(2)

  • Consider \(\mathbb{R}\) as a Lawvere metric space, i.e. as a Cost-category.

  • Form the Cost-product \(\mathbb{R}\times\mathbb{R}\).

  • What is the distance from \((5,6)\) to \((-1,4)\)?

Solution(1)

The distance is the Manhattan/\(L_1\) distance: \(|5-(-1)| + |6-4| = 8\)