The operation of joining systems earlier can be derived from a more basic structure: order.
Let \(A \leq B\) be defined as a relationship that holds when \(\forall x,y:\ (x,y) \in A \implies (x,y) \in B\)
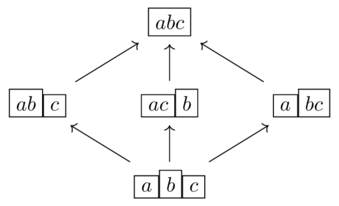
The joined system \(A \lor B\) is the smallest system that is bigger than both \(A\) and \(B\).
The possibility of a generative effect is captured in the inequality \(\phi(A) \lor \phi(B) \leq \phi(A \lor B)\), where \(\phi\) was defined earlier.
There was a generative effect because there exist systems violate this (both are individually false for \(\phi\) but not when put together).
\(\phi\) preserves order but not join