Exercise 1-101(2)
Does \(\mathbb{R}\xrightarrow{\lceil x/3 \rceil}\mathbb{Z}\) have a left adjoint \(\mathbb{Z} \xrightarrow{L} \mathbb{R}\)? If not, why? If so, does its left adjoint have a left adjoint?
Solution(1)
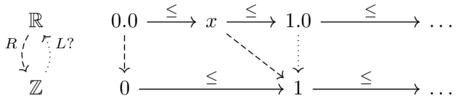
Assume we have an arbitrary left adjoint, \(L\).
For \(x\) as it approaches \(0.0 \in \mathbb{R}\) from the right, we have \(R(x) \leq 1\), therefore \(L(1) \leq x\) because \(L\) is left adjoint.
Therefore \(L(1)\leq 0.0\), yet this implies \(R(0.0) \leq 1\).
This contradicts \(R(0.0)=0\), therefore no left adjoint exists.