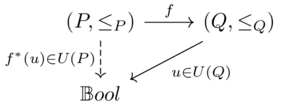Chapter 1: Generative Effects

More than the sum of their parts(6)
A first look at generative effects(3)

  • Central theme of category theory: study of structures and structure-preserving maps.

  • Asking which aspects of structure one wants to preserve becomes the question "what category are you working in?".

  • Example: there are many functions \(\mathbb{R} \xrightarrow{f} \mathbb{R}\), which we can think of observations (rather than view \(x\) directly we only view \(f(x)\)). Only some preserve the order of numbers, only some preserve distances between numbers.

  • The less structure that is preserved by our observation of a system, the more ’surprises’ when we observe its operations - call these generative effects.

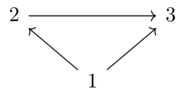
  • Consider a world of systems which are points which may or may not be connected. There are 5 partitionings or systems of three points.

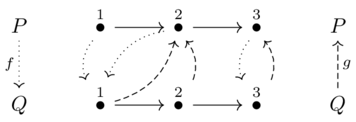
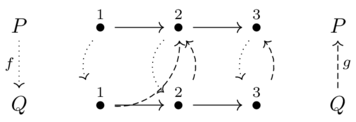
  • Suppose Alice makes observations on systems with a function \(\phi\) which returns whether or not points are connected. Alice also has an operation on two systems called join which puts two points in the same partition if they are connected in either of the original systems.

  • Alice’s operation is not preserved by the join operation.

  • Application: Alice is trying to address a possible contagion and needs to know whether or not it is safe to have each region extract their data and then aggregate vs aggregating data and then extracting from it.

Exercise 1-1(2)

Give an example and non-example for

  1. an order-preserving function

  2. a metric-preserving function

  3. an addition-preserving function

Solution(1)

  1. Order-preserving \(x+1\), non-order-preserving \(-x\)

  2. Metric preserving \(x+1\), non-metric-preserving \(2x\)

  3. Addition-preserving \(2x\), non-addition-preserving \(x^2\)

Linked by

Ordering systems(3)

  • The operation of joining systems earlier can be derived from a more basic structure: order.

  • Let \(A \leq B\) be defined as a relationship that holds when \(\forall x,y:\ (x,y) \in A \implies (x,y) \in B\)

  • The joined system \(A \lor B\) is the smallest system that is bigger than both \(A\) and \(B\).

  • The possibility of a generative effect is captured in the inequality \(\phi(A) \lor \phi(B) \leq \phi(A \lor B)\), where \(\phi\) was defined earlier.

  • There was a generative effect because there exist systems violate this (both are individually false for \(\phi\) but not when put together).

  • \(\phi\) preserves order but not join

Exercise 1-7(2)

Using the order \(false \leq true\) for \(\mathbb{B}\), what is:

  • \(true \lor false\)

  • \(false \lor true\)

  • \(true \lor true\)

  • \(false \lor false\)

Solution(1)

This is same as logical or: \(true,\ true,\ true,\ false\)

What is order(11)
Review of sets, relations functions(1)

  • Basic review of set, subset, partition, equivalence relation.

  • A partition of a set is a surjective map to the parts.

  • Any \(a \in A\) can be thought of as a function \(\{1\} \xrightarrow{a} A\)

Exercise 1-16(2)

Suppose \(A\) is a partitioned set and \(P,Q\) are two partitions such that for each \(p \in P\) there exists a \(q \in Q\) with \(A_p=A_q\)

  1. Show that for each \(p \in P\) there is at most one \(q \in Q\) such that \(A_p = A_q\)

  2. Show that for each \(q \in Q\) there is a \(p \in P\) such that \(A_p = A_q\)

Solution(1)

  1. Suppose \(q' \ne q\). If they are both equal to \(A_p\) then they are equal to each other, but a partition rule is that \(q' \ne q\) must have an empty intersection (and \(A_p\) cannot be empty by the other rule).

  2. By part 1, the mapping between part labels is a bijection, so there is an inverse map as well.

Exercise 1-20(2)

Finish proof Proposition 1.19. Suppose that \(\sim\) is an equivalence relation on a set A, and let P be the set of \(\sim\)-closed and \(\sim\)-connected subsets.

  1. Show that each part \(A_p\) is nonempty

  2. Show that \(p \ne q \implies A_p \cap A_q = \varnothing\)

  3. Show that \(A = \bigcup_{p \in P} A_p\)

Proof(1)

  1. Part of the definition of \(\sim\)-connected is being nonempty

  2. Suppose \(a \in A\) is in the intersection. Then \(a \sim p\) and \(a \sim q\) for some elements \(p \not\sim q\) arbitrarily selected from \(A_p, A_q\). But this is impossible because \(\sim\) is transitive, so this must be impossible.

    • Every \(a \in A\) is part of some equivalence class which is a \(\sim\)-closed and \(\sim\)-connected set, so \(A \subseteq \bigcup_{p \in P} A_p\)

      • The equivalence class is \(\sim\)-closed because two elements being \(\sim\)-related implies they are in the same equivalence class.

      • The equivalence class is \(\sim\)-connected because equivalence classes are nonempty and the equivalence relation is transitive.

    • The constituents of \(A_p\) were defined to be subsets of \(A\), so unioning these will also be a subset of \(A\), i.e. \(\bigcup_{p \in P} A_p \subseteq A\).

    • Therefore \(A = \bigcup_{p \in P} A_p\).

Function(1)

A function from \(S\) to \(T\)

A relation \(F \subseteq S \times T\) such that \(\forall s \in S:\ \exists! t \in T:\ (s,t) \in F\)

  • The preimage of an element \(t \in T\) is \(\{s \in S\ |\ F(s)=t\}\)

  • \(\hookrightarrow\) Injectivity: \(s\ne s' \implies F(s)\ne F(s')\)

  • \(\twoheadrightarrow\) Surjectivity: \(\forall t \in T:\ \exists s \in S:\ (s,t) \in F\)

  • \(\xrightarrow \cong\) Bijectivity: both injectivity and surjectivity.

Linked by

Partition(1)

A partition of set \(A\)

A set \(P\) (‘part labels’) and, for each \(p \in P\), a nonempty subset (‘pth part’) \(A_p \subseteq A\) such that:

  1. \(A = \bigcup_{p \in P}A_p\)

  2. \(p \ne q \implies A_p \cap A_q = \varnothing\)

Two partitions are considered the same if the partitioned groups are the same, the labels don’t matter.

Linked by

Partitions are equivalences(2)

There is a bijection between ways to partition a set \(A\) and the equivalence relations on \(A\)

Proof(1)

  • Every partition gives rise to a distinct equivalence relation

    • Define \(a \sim b\) to mean \(a,b\) are in the same part. This is a reflective, symmetric, and transitive relation given the definition of a partition.

  • Every equivalence relation gives rise to a distinct partition.

    • Define a subset \(X \subseteq A\) as \(\sim\)-closed if, for every \(x \in X\) and \(x' \sim x\), we have \(x' \in X\).

    • Define a subset \(X \subseteq A\) as \(\sim\)-connected if it is nonempty and \(\forall x,y \in X:\ x \sim y\)

    • The parts corresponding to \(\sim\) are precisely the \(\sim\)-closed and \(\sim\)-connected subsets.

Linked by

Quotient(1)

A quotient of a set under an equivalence relation.

This is equivalent to the parts of the partition associated with the equivalence relation.

Linked by

Relation(1)

A relation between sets \(X\) and \(Y\)

  • A subset \(R \subseteq X \times Y\).

  • A binary relation on \(X\) is a subset of \(X \times X\)

Linked by

Preorders(10)
Preorder(1)
Exercise 1-53(2)

For any set \(S\) there is a coarsest partition having just one part.

What surjective function does this correspond to?

(Likewise for the finest partition?)

Solution(1)

The trivial map to \(\{1\}\) and the identity, respectively.

Exercise 1-55(2)

Prove that the upper sets on a discrete preorder for some set \(X\) is simply the power set \(P(X)\)

Solution(1)

  • The upper set criterion is satisfied by any subset, thus all possible subsets are upper sets.

  • The binary relation is equality, thus the upper subset criterion becomes \(p \in U \land p = q \implies q \in U\) or alternatively \(p \in U \implies p \in U\) which is always satisfied.

Graph(1)

A graph (of vertices, arrows)

  • A tuple \(G=(V, A, s, t)\)

  • Set of vertices and arrows, with two functions \(A\rightarrow V\) which say where the source and target of each arrow goes to.

  • A path in \(G\) is any sequence of arrows such that the target of one arrow is the source of the next (including length 0 and 1 sequences).

Linked by

Opposite preorder(1)

An opposite preorder

Given a preorder \((P, \leq)\), we define \(p \leq^{op} q \iff q \leq p\)

Linked by

Skeletality(1)
Upper set(1)

An upper set in \(P\) for some preorder \((P, \leq)\)

  • A subset \(U\) of \(P\) satisfying the condition \(p \in U \land p \leq q \implies q \in U\)

  • Anything you add to the upper set means you have to add everything greater than it.

  • Example: the possible upper sets of \(Bool\) are \(\{\varnothing, \{true\}, \{true, false\}\}\)

Linked by

Monotone maps(15)
Monotone map(1)

A monotone map between preorders \((A, \leq_A), (B, \leq_B)\)

A function \(A \xrightarrow{f} B\) such that \(\forall x,y \in A: x \leq_A y \implies f(x) \leq_B f(y)\)

Linked by

Dagger preorder(1)

A dagger preorder

\(q \leq p \iff p \leq q\) - this is tantamount to an equivalence relation.

Linked by

Preorder isomorphism(1)

A preorder isomorphism

A monotone map for which there exists an inverse monotone map (\(f;g=id\) and \(g;f = id\))

  • If this exists, we say the preorders involved are isomorphic.

Linked by

Pullback along monotone(1)

A pullback along a monotone map \(P \xrightarrow{f} Q\)

  • We take the preimage of \(f\), but not for a single element of \(Q\) but rather an upper set of \(Q\).

  • Noting that upper sets are monotone maps to Bool, it follows that the result of a pullback is an upper set in \(P\) follows from the fact that composition preserves monotonicity.

  • Therefore the type of the pullback is \(U(Q) \xrightarrow{f^*} U(P)\)

Linked by

Exercise 1-66(2)

Let \((P, \leq)\) be a preorder and recall the opposite preorder.

  1. Show that the set \(\uparrow(p) := \{p' \in P\ |\ p \leq p'\}\) is an upper set for any \[p \in P\]

  2. Show that this construction defines a monotone map \((P, \leq^{op}) \xrightarrow{\uparrow} U(P)\)

  3. Show that \(p \leq p' \iff \uparrow(p') \subseteq \uparrow(p)\)

  4. Draw a picture of the map \(\uparrow\) in the case where \(P\) is the preorder \((b\geq a \leq c)\).

Solution(1)

This is the Yoneda lemma for preorders (up to equivalence, to know an element is the same as knowing its upper set).

  1. This is basically the definition an upper set starting at some element.

  2. Interpreting the meaning of the preorder in the domain and codomain of \(\uparrow\), this boils down to showing \(p \leq p'\) implies \(\uparrow(p') \subseteq \uparrow(p)\) - This is shown by noting that \(p' \in \uparrow(p)\) and anything ‘above’ \(p'\) (i.e. \(\uparrow(p')\)) will therefore be in \(\uparrow(p)\).

  3. Forward direction has been shown above - The other direction is shown just by noting that \(p\prime\) must be an element of \(\uparrow(p\prime)\) and by the subset relation also in \(\uparrow(p')\), therefore \(p \leq p'\).

Exercise 1-67(2)

Show that when \(P\) is a discrete preorder, then every function \(P \rightarrow Q\) is a monotone map, regardless of the order \(\leq_Q\).

Solution(1)

The only time the monotonicity criterion is deployed is when two elements of \(P\) are related, and for a discrete category this means we only have to check whether \(f(a) \leq_Q f(a)\), which is true because preorders are reflexive.

Exercise 1-73(2)

Recall skeletal preorders and dagger preorders.

Show that a skeletal dagger preorder is just a discrete preorder (and hence can be identified with a set)

Solution(1)

  • Because preorders are reflexive, we just have to show \(a \ne b \implies a \not\leq b\), or its contrapositive: \(a \leq b \implies a = b\).

  • \(a \leq b \overset{dagger}{\implies} b \leq a \overset{skeletal}{\implies} a = b\)

Identities are monotone(2)

  • For any preorder, the identity function is a monotone map.

  • The composition of two monotone maps (\(P \xrightarrow{f} Q \xrightarrow{g} R\)) is also monotone.

Proof(1)

  • Monotonicity translates to \(a \leq b \implies a \leq b\) and is trivially true.

  • Need to show: \(a \leq_P b \implies g(f(a)) \leq_R g(f(b))\)

    • The monotonicity of \(f\) gives us \(f(a) \leq_Q f(b)\) and the monotonicity of \(g\) gives us the result we need.

Monotones to bool(2)

Let \(P\) be a preorder. Monotone maps \(P \rightarrow \mathbb{B}\) are in one-to-one correspondance with upper sets of \(P\).

Proof(1)

  • Let \(P \xrightarrow{f} \mathbb{B}\) be a monotone map. The subset \(f^{-1}(true)\) is an upper set.

    • Suppose \(p \in f^{-1}(true)\) and \(p \leq q\).

    • Then \(true = f(p) \leq f(q)\) because \(f\) is monotonic.

    • But there is nothing strictly greater than \(true\) in \(\mathbb{B}\), so \(f(q) = true\) and therefore \(q \in f^{-1}(true)\) too.

  • Suppose \(U \in U(P)\), and define \(P\xrightarrow{f_U}\mathbb{B}\) such that \(f_U=true \iff p \in U\)

    • Given there are only two values in \(B\) and an arbitrary \(p\leq q\), the only way for this to not be monotone is for \(f_U(p) \land \neg f_U(q)\) but this defies the definition of an upper set.

  • The two constructions are mutually inverse.

Linked by

Meets and joins(14)
Definition and basic examples(9)

  • There could be multiple meets/joins, but the definition forces them to be isomorphic.

  • An arbitrary preorder need not have a meet nor join.

    • E.g a two element discrete preorder has no overall meet/join, because the meet must be less/greater than or equal to both elements in the set.

Exercise 1-85(2)

Let \(p \in P\) be an element in a preorder. Consider \(A = \{p\}\)

  1. Show that \(\wedge A \cong p\)

  2. Show that if \(P\) is a partial order, then \(\wedge A = p\)

  3. Are the analogous facts true when \(\wedge\) is replaced by \(\vee\)?

Solution(1)

    • The first condition of the meet gives us that \(\wedge A \leq p\).

    • The second condition is that \(\forall q \in P: q \leq p \implies q \leq \wedge A\).

      • Substituting \(p\) in for \(q\), the antecedent holds such that we get \(p \leq \wedge A\).

    • Therefore \(p \cong \wedge A\)

  2. The difference between a partial order and a preorder is that congruent elements are equal, so we directly get that \(p = \wedge A\)

  3. Yes, the argument is perfectly symmetric.

Meet and join(1)

For a preorder \((P, \leq)\), the meet and join of \(A \subseteq P\).

  • The meet \(\wedge A\) is an element such that

    • \(\forall a \in A: \wedge A \leq a\)

    • \(\forall q \in P: (\forall a \in A: q \leq a) \implies q \leq \wedge A\)

    • Think of as a GREATEST LOWER BOUND

  • The join \(\vee A\) is an element such that

    • \(\forall a \in A: a \leq \vee A\)

    • \(\forall q \in P: (\forall a \in A: a \leq q) \implies \vee A \leq q\)

    • Think of as a LEAST UPPER BOUND

Linked by

Meets and joins of bool(1)

In the booleans, the meet of any two elements is given by \(AND\) and the join of any two elements is given by \(OR\).

Linked by

Meets and joins of powerset(1)

In a power set, the meet of a collection of subsets is their intersection, while the join is their union.

Meets and joins of total order(1)

In a total order, the meet of a set is its infimum, while the join is the supremum.

Note that \(\mathbb{B}\) is a total order, to generalize Example 1.88.

Meets of subsets(2)

Suppose \((P,\leq)\) is a preorder and \(A \subseteq B \subseteq P\) are subsets that have meets. Then \(\bigwedge B \leq \bigwedge A\)

Solution(1)

  • Let \(m = \bigwedge A\) and \(n = \bigwedge B\).

  • For any \(a \in A\) we also have \(a \in B\), so \(n \leq A\) because \(n\) is a lower bound for \(B\).

  • Thus \(n\) is also a lower bound for \(A\) and hence \(n \leq m\) because \(m\) is \(A\)’s greatest lower bound.

Linked by

Back to observations and generative effects(5)

  • We are comparing the observation of a combined system or the combination of observations.

  • The other direction, restricting an observation of a system to a subsystem, does not have problems for monotone maps (which preserve meets, not joins).

Monotone maps that preserve meets(1)

A monotone map \(P \xrightarrow{f} Q\) that preserves meets

  • \(f(a \land_P b) \cong f(a) \land_Q f(b)\)

  • Likewise, to preserve joins is for \(f(a \lor_P b) \cong f(a) \lor_Q f(b)\)

Generative effect(1)

A monotone map \(P \xrightarrow{f} Q\) has a generative effect

\(\exists a,b \in P: f(a) \lor f(b) \not\cong f(a \lor v)\)

Linked by

Exercise 1-94(2)

Prove that for any monotone map \(P \xrightarrow{f} Q\):

  • if there exist \(a \lor b \in P\) and \(f(a) \lor f(b) \in Q\):

  • \(f(a) \lor_Q f(b) \leq f(a \lor_P b)\)

Solution(1)

  • Let’s abbreviate \(f(a\ \lor_P\ b)\) as \(JF\) (join-first) and \(f(b)\ \lor_Q\ f(a)\) as \(JL\) (join-last)

    • This exercise is to show that \(JL \leq JF\)

  • The property of joins gives us, in \(P\), that \(a\ \leq\ (a \lor b)\) and \(b\ \leq\ (a \lor b)\)

    • Monotonicity then gives us, in \(Q\), that \(f(a) \leq JF\) and \(f(b) \leq JF\)

  • We also know from the property of joins, in \(Q\), that \(f(a) \leq JL\) and \(f(b) \leq JL\)

  • The only way that \(JF\) could be strictly smaller than \(JL\), given that both are \(\geq f(a)\) and \(\geq f(b)\) is for \(f(a) \leq JF < JL\) and \(f(b) \leq JF < JL\)

  • But, \(JL \in Q\) is the smallest thing (or equal to it) that is greater than \(f(a)\) and \(f(b)\), so this situation is not possible.

Galois connections(30)
Definition and examples(5)
Exercise 1-101(2)

Does \(\mathbb{R}\xrightarrow{\lceil x/3 \rceil}\mathbb{Z}\) have a left adjoint \(\mathbb{Z} \xrightarrow{L} \mathbb{R}\)? If not, why? If so, does its left adjoint have a left adjoint?

Solution(1)

  • Assume we have an arbitrary left adjoint, \(L\).

  • For \(x\) as it approaches \(0.0 \in \mathbb{R}\) from the right, we have \(R(x) \leq 1\), therefore \(L(1) \leq x\) because \(L\) is left adjoint.

  • Therefore \(L(1)\leq 0.0\), yet this implies \(R(0.0) \leq 1\).

  • This contradicts \(R(0.0)=0\), therefore no left adjoint exists.

Floor and ceil(1)

  • Consider the map \(\mathbb{Z} \xrightarrow{3z} \mathbb{R}\) which sends an integer to \(3z\) in the reals.

  • To find a left adjoint for this map, we write \(\lceil r \rceil\) for the smallest natural above \(r \in \mathbb{R}\) and \(\lfloor r \rfloor\) for the largest integer below \(r \in \mathbb{R}\)

  • The left adjoint is \(\lceil r/3 \rceil\)

  • Check: \(\lceil x/3 \rceil \leq y\) \(\iff x \leq 3y\)

Galois connection(1)
Total order galois connections(1)

  • Consider the total orders \(P = Q = \underline{3}\) with the following monotone maps:

  • These maps do not form a Galois connection:

    • These do not because of \(p=2, q = 1\)

    • \(f(p)=2 \not \leq q=1\) which is not the same as \(p = 1 \leq g(q)=2\)

  • In some sense that can be formalized, for total orders the notion of Galois connection corresponds to the maps not ‘crossing over’.

Back to partitions(3)

  • Given any function \(S \xrightarrow{g} T\), we can induce a Galois connection \(Prt(S) \leftrightarrows Prt(T)\) between the sets of partitions of the domain and codomain.

    • Determine the left adjoint \(Prt(S) \xrightarrow{g_!} Prt(T)\)

      • Starting with a given partition in \(S\), obtain a partition in \(T\) by saying two elements, \(t_1,t_2\) are in the same partition if \(\exists s_1 \sim s_2: g(s_1)=t_1 \land g(s_2)=t_2\)

      • This is not necessarily a transitive relation, so take the transitive closure.

    • Determine the right adjoint \(Prt(T) \xrightarrow{g^*} Prt(S)\)

      • Given a partition of \(T\), we say two elements in \(S\) are connected iff \(g(s_1) \sim g(s_2)\)

Exercise 1-106(2)

Given a function \(\{1 \mapsto 12, 2 \mapsto 12, 3 \mapsto 3, 4 \mapsto 4\}\) from the four element set \(S\) to the three element set \(T\)

  1. Choose a nontrivial partition \(c \in Prt(S)\) and compute \(g_!(c) \in Prt(T)\)

  2. Choose any coarser partition \(g_!(c)\leq d \in Prt(T)\)

  3. Choose any non-coarser partition \(g_!(c) > e \in Prt(T)\)

  4. Find \(g^*(d)\) and \(g^*(e)\)

  5. Show that the adjunction formula is true, i.e. that \(c \leq g^*(d)\) (because \(g_!(c) \leq d\)) and \(g^*(e) > c\) (because \(e > g_!(c)\))

Solution(1)

  1. \(c = \{(1, 3),(2,), (4,)\}\), \(g_!(c)\) is then \(\{(12,3),(4,)\}\)

  2. \(d = \{(12,),(3,),(4,)\}\)

  3. \(e = \{(12,3,4)\}\)

  4. \(g^*(d)=\{(1,2),(3,),(4,)\}, g^*(e)=\{(1,2,3,4)\}\)

  5. \(c \leq g^*(d)\) and \(g^*(e) > c\)

Basic theory of Galois connections(12)
Galois connection alternate form(2)

Suppose \(P \overset{g}{\underset{f}{\leftrightarrows}} Q\) are monotone maps. The following are equivalent:

Proof(1)

  • Forward direction

    • Take any \(p \in P\) and let \(q = f(p) \in Q\)

      • By reflexivity, we have in \(Q\) that \(f(p) \leq q\)

      • By definition of Galois connection, we then have \(p \leq g(q)\), so (1) holds.

    • Take any \(q \in Q\) and let \(p = g(q) \in P\)

      • By reflexivity, we have in \(P\) that \(p \leq g(q)\)

      • By definition of Galois connection, we then have \(f(p) \leq q\), so (2) holds.

  • Reverse direction

    • Want to show \(f(p)\leq q \iff p \leq g(q)\)

    • Suppose \(f(p) \leq q\)

      • Since g is monotonic, \(g(f(p)) \leq g(q)\)

      • but, because (1), \(p \leq g(f(p))\), therefore \(p \leq g(q)\)

    • Suppose \(p \leq g(q)\)

      • Since f is monotonic, \(f(p) \leq f(g(q))\)

      • but, because (2), \(f(g(q)) \leq q\), therefore \(f(p) \leq q\)

Linked by

Adjoints preserving meets and joins(2)

  • Let \(P \overset{f}{\underset{g}{\rightleftarrows}} Q\) be monotone maps with \(f \dashv g\).

  • Right adjoints preserve meets

    • Suppose \(A \subseteq Q\) is any subset and \(g(A)\) is its image.

    • Then, if \(A\) has a meet \(\wedge A \in Q\), then \(g(A)\) has a meet \(\wedge g(A) \in P\)

    • And \(g(\wedge A) \cong \wedge g(A)\)

  • Left adjoints preserve joins

    • Given \(A \subseteq P\) and its image \(f(A) \subseteq Q\)

    • Then, if \(A\) has a join \(\vee A \in P\), then \(\vee f(a) \in Q\) exists

    • And \(f(\vee A) \cong \vee f(A)\)

Proof(1)

  • Left adjoints preserve joins

    • let \(j = \vee A \subseteq P\)

    • Given f is monotone, \(\forall a \in A: f(a) \leq f(j)\), i.e. we have \(f(a)\) as an upper bound for \(f(A)\)

    • To show it is a least upper bound, take some arbitrary other upper bound b for \(f(A)\) and show that \(f(j) \leq b\)

      • Because \(j\) is the least upper bound of \(A\), we have \(j \leq g(b)\)

      • Using the Galois connection, we have \(f(j) \leq b\) showing that \(f(j)\) is the least upper bound of \(f(A) \subseteq Q\).

  • Right adjoints preserving meets is dual to this.

Linked by

Adjoint functor theorem for preorders(2)
Proof(1)

  • Given a right adjoint, construct the left adjoint by:

    • \(f(p) := \bigwedge\{q \in Q\ |\ p \leq g(q)\}\)

    • First need to show this is monotone:

      • If \(p \leq p'\), the relationship between the joined sets of \(f(p)\) and \(f(p')\) is that the latter is a subset of the former.

      • By Proposition 1.91 we infer that \(f(p) \leq f(p')\).

    • Then need to show that it is satisfies the left adjoint property:

      • Show that \(p_0 \leq g(f(p_0))\)

        • \(p_0 \leq \bigwedge \{g(q)\ |\ p_0 \leq g(q)\} \cong g(\bigwedge\{q\ |\ p_0 \leq g(q)\}) = g(f(p_0))\)

        • The first inequality comes from the fact that the meet of the set (of which \(p_0\) is a lower bound) is a greatest lower bound.

        • The congruence comes from the fact that right adjoints preserve meets.

      • Show that \(f(g(q_0)) \leq q_0\)

        • \(f(g(q_0)) = \bigwedge\{q\ |\ g(q_0) \leq g(q)\} \leq \bigwedge \{q_0\} = q_0\)

        • The first inequality comes from Proposition 1.91 since \(\{q_0\}\) is a subset of the first set.

        • The second equality is a property of the meet of single element sets.

  • Proof of a left adjoint construction (assuming it preserves joins) is dual.

Linked by

Adjoints in Set(1)

  • Let \(A \xrightarrow{f} B\) be a set function, say between apples and buckets into which we put each apple.

  • The ‘pullback along f’ \(\mathbb{P}(B) \xrightarrow{f^*} \mathbb{P}(A)\) maps each subset \(B' \subseteq B\) to its preimage \(f^{-1}(B') \subseteq A\)

    • It tells you for a set of buckets all the apples contained in total.

    • It is a monotonic map which has a left and right adjoint: \(f_! \dashv f^* \dashv f_*\)

  • The left adjoint \(\mathbb{P}(A)\xrightarrow{f_!}\mathbb{P}(B)\) is given by the direct image

    • \(f_!(A') := \{b \in B\ |\ \exists a \in A': f(a)=b\}\)

    • Tells you for a set of apples all the buckets that contain at least one of those apples.

  • The right adjoint \(\mathbb{P}(A) \xrightarrow{f_*} \mathbb{P}(B)\) is defined as follows:

    • \(f_*(A') := \{b \in B\ |\ \forall a: f(a)=b \implies a \in A'\}\)

    • Tells you all the buckets which are all-\(A\prime\) (note that empty buckets vacuously satisfy this condition).

  • Adjoints often turn out to have interesting semantic interpretations.

Exercise 1-110(2)

Show that if \(P \xrightarrow{f}Q\) has a right adjoint g, then it is unique up to isomorphism. Is the same true for left adjoints?

Solution(1)

  • Suppose \(h\) is also right adjoint to \(f\).

  • What it means for \(h \cong g\):

    • \(\forall q \in Q: h(q) \cong g(q)\)

  • \(g(q) \leq h(q)\)

    • Substitute \(g(q)\) for \(p\) in \(p \leq h(f(p))\) (from \(h\)’s adjointness) to get \(g(q) \leq h(f(g(q)))\)

    • Also apply \(h\) to both sides of \(f(g(q)) \leq q\) (from \(g\)’s adjointness) to get \(h(f(g(q)))\leq h(q)\)

    • The result follows from transitivity.

  • By symmetry (nothing was specified about \(h\) or \(g\)) the proof of \(h(q)\leq g(q)\) is the same.

  • Same reasoning for left adjoints.

Exercise 1-118(2)

Choose sets \(X,Y\) with between two and four elements each, and choose a function \(X \xrightarrow{f} Y\) NOCARD

  1. Choose two different subsets \(B_1, B_2 \subseteq Y\) and find \(f^*(B_1)\) and \(f^*(B_2)\)

  2. Choose two different subsets \(A_1, A_2 \subseteq X\) and find \(f_!(A_1)\) and \(f_!(A_2)\)

  3. With the same \(A_1, A_2\) find \(f_*(A_1)\) and \(f_*(A_2)\)

Solution(1)

\(\bar 3 \xrightarrow{f} \bar 4\) with \(\{1 \mapsto 2, 2 \mapsto 2, 3\mapsto 4\}\),\(A_1 = \{1,2\}, A_2=\{2,3\}, B_1=\{1\}, B_2=\{1,4\}\)

  1. \(f^*(B_1)=\varnothing, f^*(B_2)=\{4\}\)

  2. \(f_!(A_1)=\{2\},f_!(A_2)=\{2,4\}\)

  3. \(f_*(A_1)=\{1,2,3\},f_*(A_2)=\{1,3,4\}\)

Closure operators(7)

Given a Galois connection we can compose the left and right maps to get a closure operator

Closure operator(1)

A closure operator \(P \xrightarrow{j} P\) on a preorder \(P\)

A monotone map such that for all \(p \in P\) we have:

  1. \(p \leq j(p)\)

  2. \(j(j(p)) \cong j(p)\)

Linked by

Eval as closure(1)

  • Example of a closure operator

  • Think of the preorder of arithmatic expressions such as \(12, 4+2+4, 9*(2+3)\), where the \(\leq\) operators denotes whether an expression can be simplified to another.

  • A computer program \(j\) that evaluates expressions is a monotonic function on the preorder to itself (if you can reduce x to y, then \(j(x)\) should be able to be rewritten as \(j(y)\).

  • The requirements of closure operator say that \(j\) should be a simplification, and that trying to reduce an expression which has already been reduced will do nothing further.

Adjunctions from closures(1)

  • Just as adjunctions give rise to closure operators, from every closure operator we may construct an adjunction.

  • Let \(P \xrightarrow{j} P\) be a closure operator.

  • Get a new preorder by looking at a subset of \(P\) fixed by \(j\).

    • \(fix_j\) defined as \(\{p \in P\ |\ j(p)\cong p\}\)

  • Define a left adjoint \(P \xrightarrow{j} fix_j\) and right adjoint \(fix_j \xhookrightarrow{g} P\) as simply the inclusion function.

  • To see that \(j \dashv g\), we need to verify \(j(p) \leq q \iff p \leq q\)

    • Show \(\rightarrow\):

      • Because \(j\) is a closure operator, \(p \leq j(p)\)

      • \(j(p) \leq q\) implies \(p \leq q\) by transivity.

    • Show \(\leftarrow\):

      • By monotonicity of \(j\) we have \(p \leq q\) implying \(j(p) \leq j(q)\)

      • \(q\) is a fix point, so the RHS is congruent to \(q\), giving \(j(p) \leq q\).

Closures in logic(1)

  • Examples of closure operators from logic.

  • Take set of all propositions as a preorder, where \(p \leq q\) iff \(p\) implies \(q\).

  • Some modal operators are closure operators

  • E.g. \(j(p)\) means “Assuming Bob is in Chicago, p”

    • \(p \implies j(p)\) (the logic is monotonic, adding assumptions does not make something true into something false.

    • \(j(j(p)) = j(p)\) (the assumption is idempotent)

Exercise 1-119(2)

Given \(f \dashv g\), prove that the composition of left and right adjoint monotone maps is a closure operator

  1. Show \(p \leq (f;g)(p)\)

  2. Show \((f;g;f;g)(p) \cong (f;g)(p)\)

Solution(1)

  1. This is one of the conditions of adjoint functors: \(p \leq g(f(p))\)

    • The \(\leq\) direction is an extension of the above: \(p \leq g(f(p)) \leq g(f(g(f(p))))\)

    • Galois property: \(q \geq f(g(q))\), substitute \(f(p)\) for \(q\) to get \(f(p) \geq f(g(f(p)))\).

    • Because \(g\) is a monotone map, we can apply it to both sides to get \(g(f(p)) \geq g(f(g(f(p))))\)

Level shifting(3)
Preorder of relations(1)

  • ‘Level shifting’

  • Given any set \(S\), there is a set \(\mathbf{Rel}(S)\) of binary relations on \(S\) (i.e. \(\mathbb{P}(S \times S)\))

  • This power set can be given a preorder structure using the subset relation.

  • A subset of possible relations satisfy the axioms of preorder relations. \(\mathbf{Pos}(S) \subseteq \mathbb{P}(S \times S)\) which again inherits a preorder structure from the subset relation

    • A preorder on the possible preorder structures of \(S\), that’s a level shift.

  • The inclusion map \(\mathbf{Pos}(S) \hookrightarrow \mathbf{Rel}(S)\) is a right adjoint to a Galois connection, while its left adjoint is \(\mathbf{Rel}(S)\overset{Cl}{\twoheadrightarrow} \mathbf{Pos}(S)\) which takes the reflexive and transitive closure of an arbitrary relation.

Exercise 1-125(2)

Let \(S=\{1,2,3\}\)

  1. Come up with any preorder relation on \(S\), and define \(U(\leq):=\{(s_1,s_2)\ |\ s_1 \leq s_2\}\) (the relation ‘underlying’ the preorder. Note \(\mathbf{Pos}(S) \xhookrightarrow{U} \mathbf{Rel}(S)\))

  2. Pick binary relations such that \(Q \subseteq U(\leq)\) and \(Q' \not \subseteq U(\leq)\)

We want to check that the reflexive/transitive closure operation \(Cl\) is really left adjoint to the underlying relation \(U\).

  • The meaning of \(Cl \dashv U\) is \(Cl(R) \sqsubset \leq \iff R \sqsubset U(\leq)\), where \(\sqsubset\) is the order relation on \(\mathbf{Pos}(S)\)

  1. Concretely show that \(Cl(Q) \sqsubset \leq\)

  2. Concretely show that \(Cl(Q') \not \sqsubset \leq\)

Solution(1)

  1. Let the preorder be given by this diagram (with implicit reflexive arrows):

  2. Let \(Q\) be given by the following diagram

    • and let \(Q'=S\times S\)

  3. \(Cl(Q) = \{11,12,22,33\}\) \(\sqsubset\) \(\leq = \{11,22,33,12,23,13\}\)

  4. \(Cl(Q') = Q' = S \times S\) \(\not \sqsubset\) \(\leq\) (reason: \((3,1) \in S \times S\) but \((3,1) \not \in \leq\))