Incrementalized queries in adhesive categories

Kris Brown


(press s for speaker notes)

5/1/25

Obligatory slide

Transitive closure

path(u,v) :- edge(u,v)
path(u,v) :- edge(u,w), path(w, v)

Overview

$$

$$

In a very generic setting, we can formulate an incremental search problem and its solution.

• General, but concrete enough that we obtain an algorithm which can be efficiently instantiated in a wide variety of settings.

• The examples queries being incrementalized are conjunctive queries of relational databases

• In particular: directed multigraphs where schema is \(\boxed{Edge \overset{s}{\underset{t}{\rightrightarrows}} Vertex}\)

The problem we address is one where changes are induced by rewrite rules. We want to leverage our knowledge of which rule which induced the change to more efficiently update queries with respect to the change.

Applications: e-graphs, compiler optimizations, database chase, agent-based model simulations

I’m going to define a special kind of incremental search problem. It’s important that it’s formulated and solved for arbitrary adhesive categories: this is good because we can get to the essence of the problem without fussing with implementation details, and we can apply it in a wide variety of contexts. The solution will have a concrete construction which should make it easy to write a real, performant, imperative algorithm given any particular domain we think of as an adhesive category.

What’s atypical about the problem I’ll solve is that it presumes the changes to the object we’re querying are induced by “rewrite rules”, which are pattern-replacement pairs which we know ahead of time. This is a kind of “double differentiation”.

Dictionary for category theory concepts

Informal term	Categorical analogue
Setting for incremental search problem	An (adhesive) category \(\mathsf{C}\)
Pattern / Query	An object, \(X \in \operatorname{Ob}\mathsf{C}\)
State of the world / set of facts	An object \(G \in \operatorname{Ob}\mathsf{C}\)
Pattern match of \(X\) in \(G\)	A morphism \(X \rightarrow G\)
Answer set to a query \(X\) in state \(G\)	\(\operatorname{Hom}_\mathsf{C}(X,G)\)
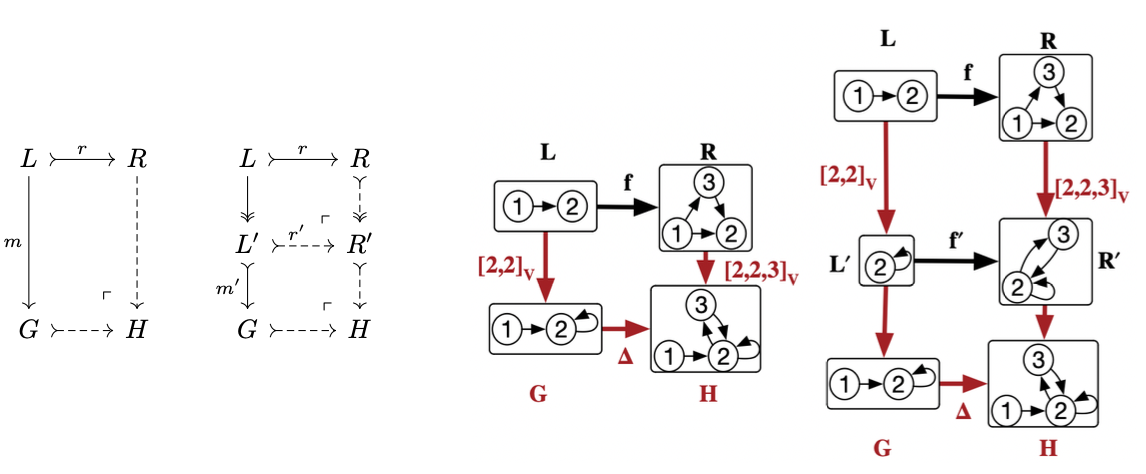
An (additive) rewrite rule, with pattern \(L\) and replacement \(R\)	A monomorphism \(f: L \rightarrowtail R\)
Application of a rewrite rule \(f\) to state \(G\) with \(L\) matched via \(m\)	A pushout of \(f\) and \(m\)

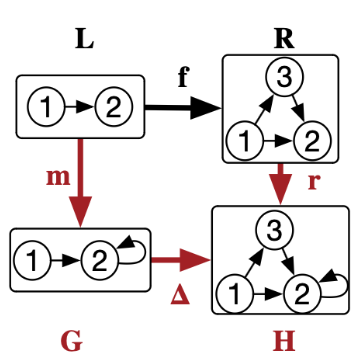
Incremental search problem: given \((G, H, m, \Delta, r)\), compute \(\operatorname{Hom}(X,H)\setminus \operatorname{Hom}(X,G)\cdot\Delta\)

Use only operations that scale with small objects (\(X,L,R\))

A repeated theme of this conference has been that it’s nice when you represent your facts in the same data structure as your data.

[Point out where all these concepts live in Figure 3.]

Note black here are things we know at compile time, red are things we know at ‘runtime’.

Another example

\[\textbf{Schema}\]

E.g. a rule which matches pairs \((A\times C)+(B\times C)\) and \((A+B)\times C\) and merges their e-classes.

Computational considerations

Objects in patterns and rules (\(L, R, X\)) are small.

The states being updated by rewrite rules (\(G, H\)) are large.

It’s computationally difficult to compute the answer set to a query \(\operatorname{Hom}(A,B)\) when \(B\) is large even when \(A\) is small (subgraph isomorphism problem); however, it’s easy to solve the rooted subgraph isomorphism problem so long as \(A\) is small.

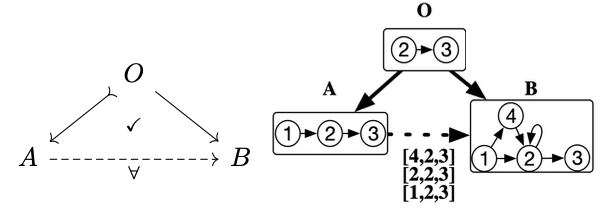
Such a partial map specifies a rooted homomorphism search problem when the monic map is componentwise connected, i.e. there exists no connected component of \(A\) which lies entirely outside the image of \(O\).

The core reason the algorithm is efficient is that it transforms something analogous to a subgraph isomorphism problem into a collection of rooted subgraph isomorphism problems. This is also a good example of how we can specify something abstractly, such as a partial map from \(A\) to \(B\), and leave it as a context-specific implementation detail of how one actually finds all of the maps from \(A\) to \(B\) consistent with that partial map.

Working backwards towards a solution

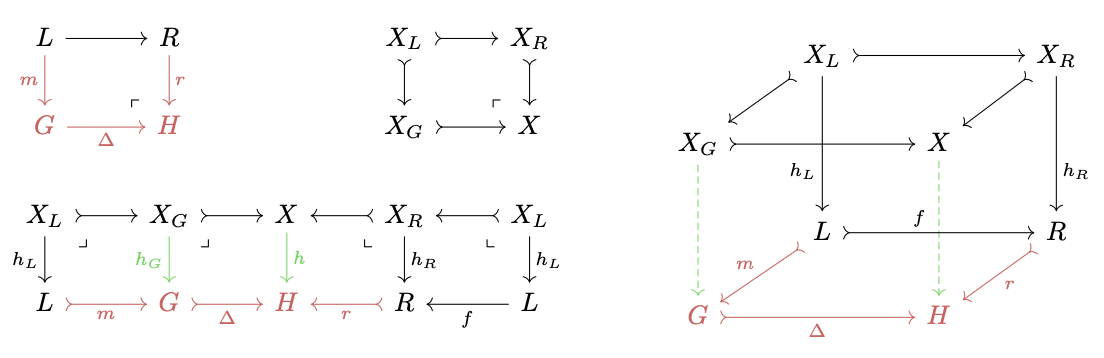
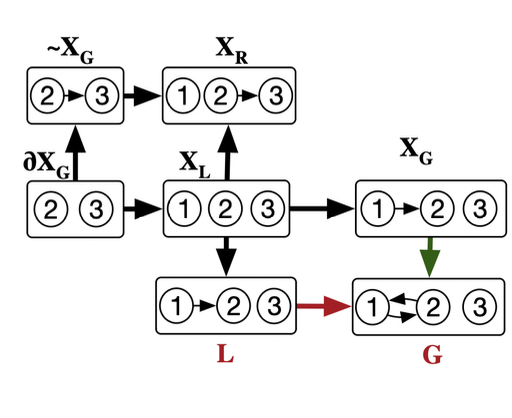
For any newly introduced match into the result of a rewrite, we have a canonical decomposition of our pattern into various subobjects.

This is a cube where the top and bottom are pushouts and the sides are all pullbacks.¹

How much of this cube can be compute at compile time?

The basic conditions of an adhesive category allow us to do the following for an arbitrary map X -> H.

The result of the rewrite is R and G glued together by L. Our pattern is also the part which intersects with Rs, the part which intersects with G, glued together by the part which intersects with L. So every match has an associated cube.

We don’t know G or H at runtime, so all their incident maps aren’t something we can precompute. But the rest of the cube is fair game.

1. I call this the adhesive cube induced by \(h\).

Example subobjects of a pattern

Top face of any cube will involve the choice of three of these elements.

The simple algorithm

At compile time

1. Enumerate all possible top faces (decompositions \(X = X_G +_{X_L} X_R\))
2. Enumerate all possible side faces above the rewrite rule:
   • For each \(X_L\rightarrowtail X_R\) and each rewrite rule \(f\), enumerate all possible maps \(h_L: X_L\rightarrow L\) and \(h_R: X_R\rightarrow R\) such that a pullback square is formed.

One of these decompositions is bad: it has \(X_G=X\): this is saying the match lies entirely in \(G\).

At runtime: for each partial cube

Given \(m\) and \(\Delta\), we can compute all possible \(h_G: X_G\rightarrow G\) over the match via a rooted search problem, only keeping the ones which form a pullback square.

Then, \(h=[h_G\cdot \Delta, h_R\cdot r]\).

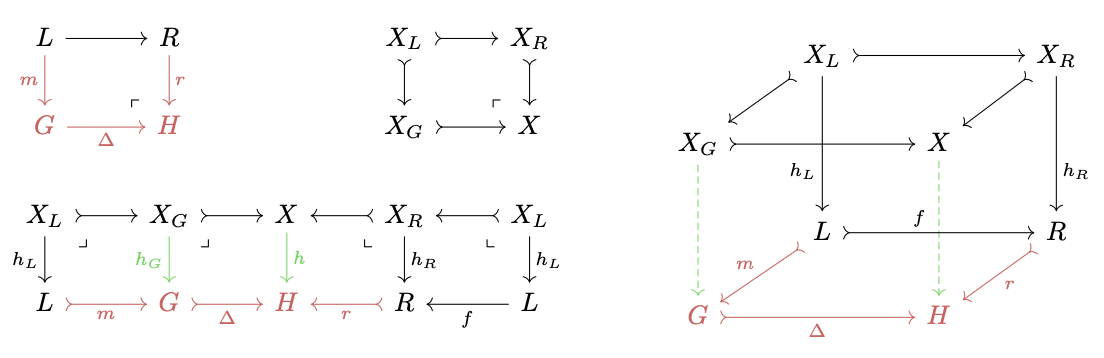
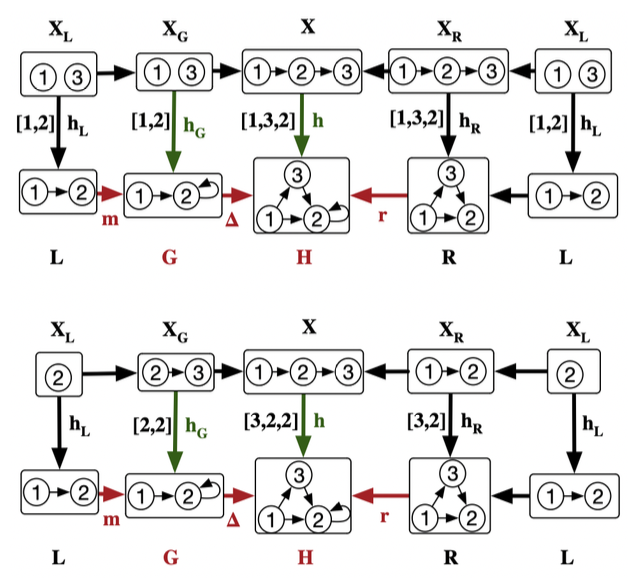
Example: finding newly introduced paths of length 2

Finding paths of length two that are introduced by the rewrite on the left. Top A choice of decomposition and interaction that recovers the match [1, 3, 2]. The decomposition asserts that the beginning and end vertex of the path will live in G, but the middle vertex and both edges will come from material newly added by the rule. Note in his case, the partial map XG → G is a total map, so there is always a unique hG (and h) associated with this rewrite. Bottom A choice of decomposition and interaction that recovers the match [3, 2, 2]. The decomposition asserts that the second edge of the path will live in G, but the first vertex and edge will come from material newly added by the rule. The search for hG candidates induced by the partial map XG → G looks for outgoing edges from 2 in G.

Correctness

That this procedure recovers exactly the new matches (i.e. \(Hom(X,H)\setminus Hom(X,G)\cdot\Delta\)) is clear: each new match corresponds to a cube, and we efficiently enumerate all possible cubes (deliberately excluding the ones which factor through \(\Delta\)).

That this is efficient requires showing that the search for \(h_G\) is always a rooted search problem, i.e. \(X_L \rightarrowtail X_G\) is componentwise connected. First, \(X_R\) is nonempty because we ruled out the trivial decomposition. Then, because \(X\) is connected and \(X \cong X_G +_{X_L} X_R\), if some disconnected component of \(X_G\) were not in the image of \(X_L\), it would remain a disconnected component in X.

It’s not a problem if we restrict attention to connected patterns \(X\), since if \(X = X_1+X_2\), we can separately update \(\operatorname{Hom}(X_1,G)\) and \(\operatorname{Hom}(X_2,G)\).

\[\operatorname{Hom}(X_1+X_2,G) \cong \operatorname{Hom}(X_1,G) \times \operatorname{Hom}(X_2,G)\]

Is it faster than seminaive?

Prefactors! This is WIP, datalog experiments are TBD.

An optimization when \(\mathsf{C}\) has complements

We can be faster in two ways: 1. there are a lot of ways to express \(X\) as a pushout that we have to iterate over. 2. it might seem wasteful that we had to filter \(h_G\) candidates by those which formed a pullback square.

Definitions

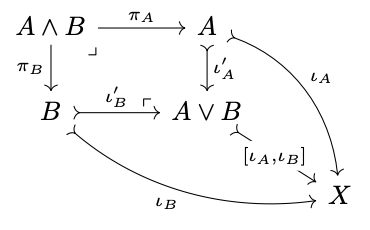
The union of two subobjects is computed by gluing them together along their intersection.

The complement of \(A\), denoted \({\sim}A\), is the smallest subobject for which \(X = A ∨ {\sim}A\).

The boundary of \(A\), denoted \(\partial A\) is \(A \wedge {\sim} A\).

Optimized algorithm: we’ll also solve the problem if we use the same algorithm

1. Only consider decompositions where \(X_R = {\sim}X_G\).
2. Keep all of the the extensions of the partial map \(h_G: X_G \leftarrowtail X_L \rightarrow G\).

Why is the optimization correct?

For any match \(h: X\rightarrow H\), we have not only a unique adhesive cube, but also what a unique minimal adhesive cube which one gets from composing two cubes together like in the below diagram:

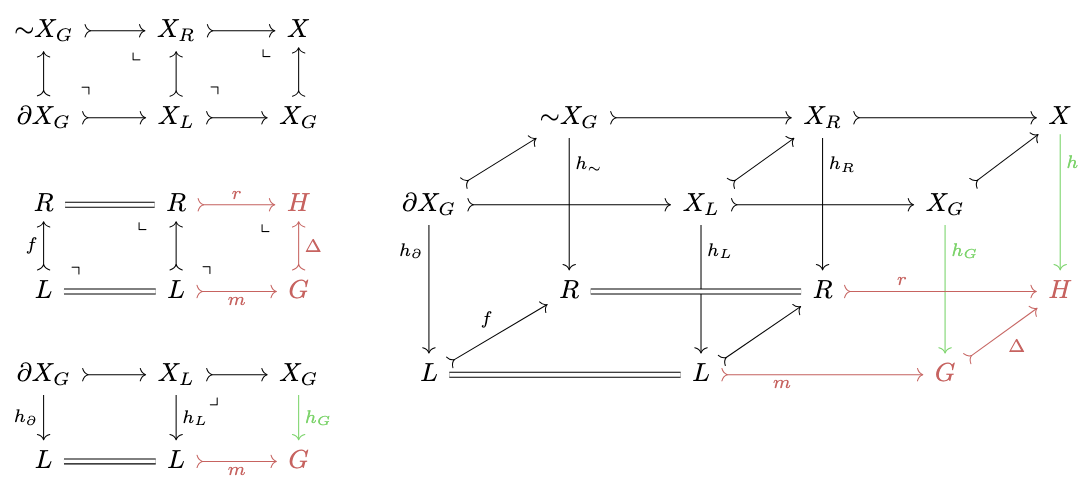
Note we can see this arbitrary \(h\) has a unique associated interaction between \(\partial X_G \rightarrowtail {\sim}X_G\) and \(f\), i.e. a pair of maps \((h_\partial, h_\sim)\) that forms a pullback with \(f\). We get this by precomposing \(h_l\) and \(h_r\) with \(\partial X_G \rightarrowtail X_L\) and \({\sim}X_G \rightarrowtail X_R\) respectively.

Iterating over minimal adhesive cubes is much nicer than iterating over adhesive cubes.

So the algorithm is structurally the same: each h has a unique cube associated with it, so loop over all partial cubes and try to complete them. But it’s nicer to loop over partial minimal adhesive cubes because the possible top faces are generally are a small subset of all possible decompositions of X. Also, the way to complete these cubes is simply looking for maps h_G which extend the partial map X_G <-< ∂ X_G {h∂;m}-> G (no filter step necessary). By the same argument as above, this partial map induces a rooted search problem because X is connected and we are excluding the trivial decomposition.

Optimized algorithm example

Let X be a path of length two. Let f be a rule which adds an edge between v2 and v3 of L. This XG says we seek new X matches which go from the target of an preexisting edge into an preexisting vertex. The minimal interaction for (XG,f) says that v2 and v3 appear in the pattern of our rewrite rule. Any interaction has to at least include v2 and v3 in its XL. The pullback condition says that, moreover, v1 doesn’t appear in the pattern. Because of this, Algorithm 3.1 would not find the match associated with hG = [1, 2, 3] depicted in this figure from the minimal interaction. Instead, that map hG would have been detected by the interaction with XL and XR also shown in the figure. The core idea of this optimization is that one doesn’t need to distinguish special cases for whether v1 appears in the pattern or not.

Batch update from multiple rule firings

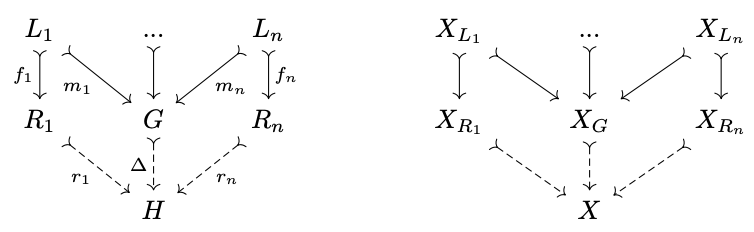
A match into the result of multiple simultaneous rewrites has a corresponding decomposition of the pattern into a colimit of subobjects of the same shape.

Our algorithm generalizes: at compile time enumerate possible decompositions of the above shape and all interactions with rewrite rules. At runtime, loop over possible partial ‘multicubes’ and look for morphisms \(h_G: X_G\rightarrow G\) that lead to pullback faces above all of the matches, which uniquely result in new matches \(h=[h_G\cdot \Delta, h_{r,1}\cdot r_1, ...]\).

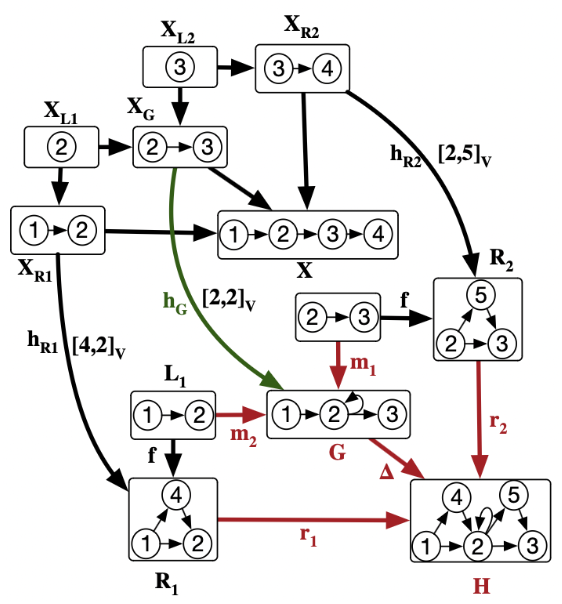
\[n=2\]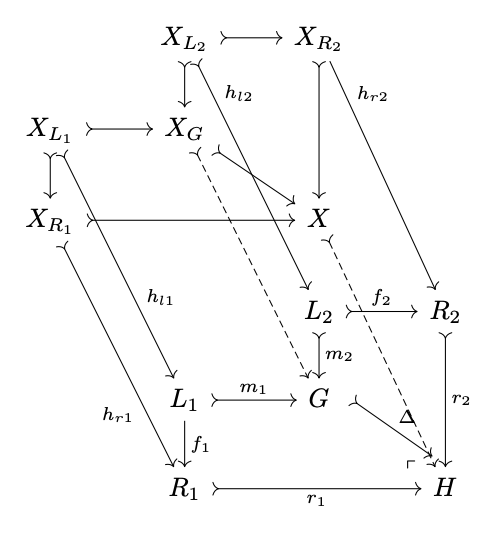

Batch example

Note the maps hl,i are not visualized to reduce clutter. The resulting match [4, 2, 2, 5] found by the decomposition of X on top is one which involves contributions from two different rule applications in the batch. The middle edge in the pattern X comes from the loop of the old graph, whereas the first and last vertices and edges are respectively created via the two rule applications.

Nonmonic matches

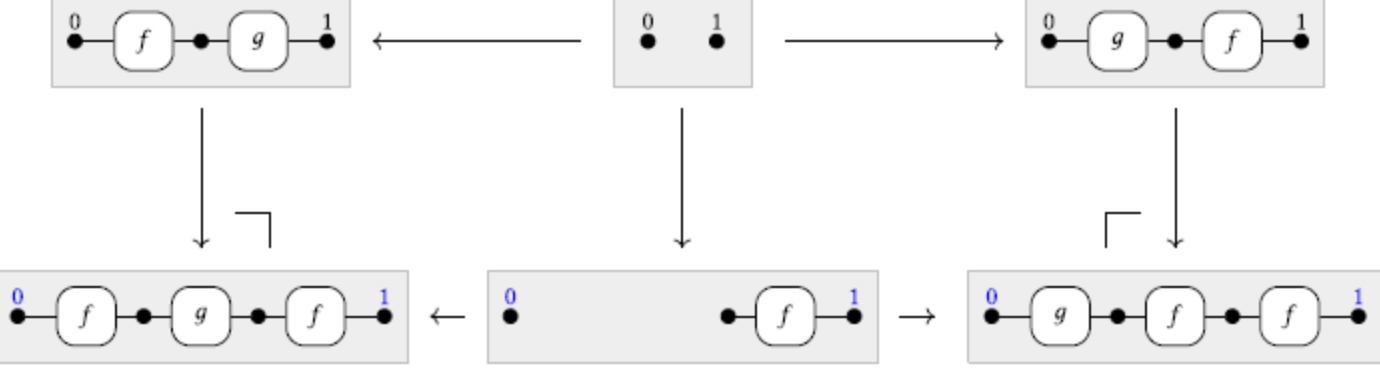
Nonmonic matches can implicitly quotient parts of the pattern, leading to new possible ways a match for a pattern \(X\) could be created. For every possible \(L\twoheadrightarrow L'\), we can compute the corresponding quotiented rule at compile time. At runtime, we epi-mono factorize any nonmonic match and use the previous algorithm with the quotiented rule.

. Left The incremental update (f : L ↣ R,m : L → G) is transformed into an update (f′ : L′ ↣ R′,m′ : L′ ↣ G) such that applying the modified rule f′ produces the same ∆ : G ↣ H. We can replace the pushout square on the left with the one on the right and then ignore the top pushout square. We can pretend our rewrite rule was r′ all along, now with a monic match m′. Right A specific example with graphs.

Merging

Everything said so far goes through when \(f\) is not monic.

• Adhesive categories still guarantee the existence of the adhesive cube.

However:

• It becomes more complicated in practice to enumerate possible top faces.
• The condition for a decomposition to be “trivial” is less simple to state.
• The condition for the optimization with complements is less simple to state.

Deletion

We can also use rewrite rules to delete (via a pushout complement).

Can state abstractly when a match has been deleted: pullback along the deletion is an iso.

However, many applications do not require deletion (e.g. the chase, e-graphs). Also many data structures can implement a form of “mark as deleted” that makes it trivial to check whether a match has been invalidated: lazily check any particular match to see if it refers to something marked as deleted.

Conclusion

• Adhesive categories are a general setting for reasoning about pattern matching and term manipulation.

  • Computational primitives we assume can be implemented efficiently in any domain of interest: 1.) computing decompositions of an object into subobjects, 2.) extending a partial map into total ones (rooted hom search), 3.) computing small (co)limits.

• We can systematically transform subgraph isomorphism problems into rooted ones.

• We can leverage information beyond the extensional difference of an update.

• Solving the base problem can be straightforwardly generalized to non-monic matches, non-connected patterns, batch updates.

• In cases where one can compute complements to subobjects, we can be more efficient.

There is an implementation in AlgebraicRewriting.jl in arbitrary \(\mathsf{C}\)-Set categories: i.e. relational databases with a fixed schema, \(\mathsf{C}\).

\[\textbf{Thank you!}\]