Agent-Based Modeling via graph rewriting
Kris Brown

(press s for speaker notes)
5/31/24
Outline
$$
$$
I. Motivation
II. AlgebraicRewriting overview
III. Agent-based programming
IV. Agent-based modeling
Goal: modeling framework which facilitates
comparing
combining
editing
visualizing
I. Motivation - examples
- Game of Life
- COVID modeling
- Discrete Lotka Volterra

I. Motivation - examples
Schema
Dynamics
Control flow
- Discrete Lotka Volterra (link)
breed [ sheep a-sheep ] ; sheep subtype of turtle
breed [ wolves wolf ] ; wolf subtype of turtle
turtles-own [ energy ] ; add energy attr to W + S
patches-own [ countdown ] ; add countdown attr to gridI. Motivation - examples
- COVID modeling (link)
Schema
mutable struct PoorSoul <: AbstractAgent
id::Int
pos::NTuple{2,Float64}
vel::NTuple{2,Float64}
mass::Float64
days_infected::Int # number of days since is infected
status::Symbol # :S, :I or :R
β::Float64
endDynamics
function elastic_collision!(a, b)
v1, v2, x1, x2 = a.vel, b.vel, a.pos, b.pos
length(v1) != 2 && error("This works only for 2D")
r1 = x1 .- x2; r2 = x2 .- x1
!(dot(r2, v1) > 0 && dot(r2, v1) > 0) && return false
dx,dv = a.pos .- b.pos, a.vel .- b.vel
n = norm(dx)^2
n == 0 && return false # do nothing if at the same pos.
a.vel = v1 .- ( dot(v1 .- v2, r1) / n ) .* (r1)
b.vel = v2 .- ( dot(v2 .- v1, r2) / n ) .* (r2)
return true
endControl flow
- Discrete Lotka Volterra (link)
Schema
breed [ sheep a-sheep ] ; sheep subtype of turtle
breed [ wolves wolf ] ; wolf subtype of turtle
turtles-own [ energy ] ; add energy attr to W + S
patches-own [ countdown ] ; add countdown attr to gridDynamics
to eat-sheep ; wolf procedure
let prey one-of sheep-here ; grab a random sheep
if prey != nobody [
ask prey [ die ] ; eat it
set energy energy + wolf-gain-from-food ; get energy
]
endControl flow
I. Challenges with getting engineers into graph rewriting
The syntax of graph rewrite rules has the virtues we want, but:
- It is a syntax for atomic changes. Nondeterminism from match and rule choice.
- Engineers / modelers need more determinism / coordinated rewriting.
What is a good syntax for talking about the algorithmic application of rewrite rules?1
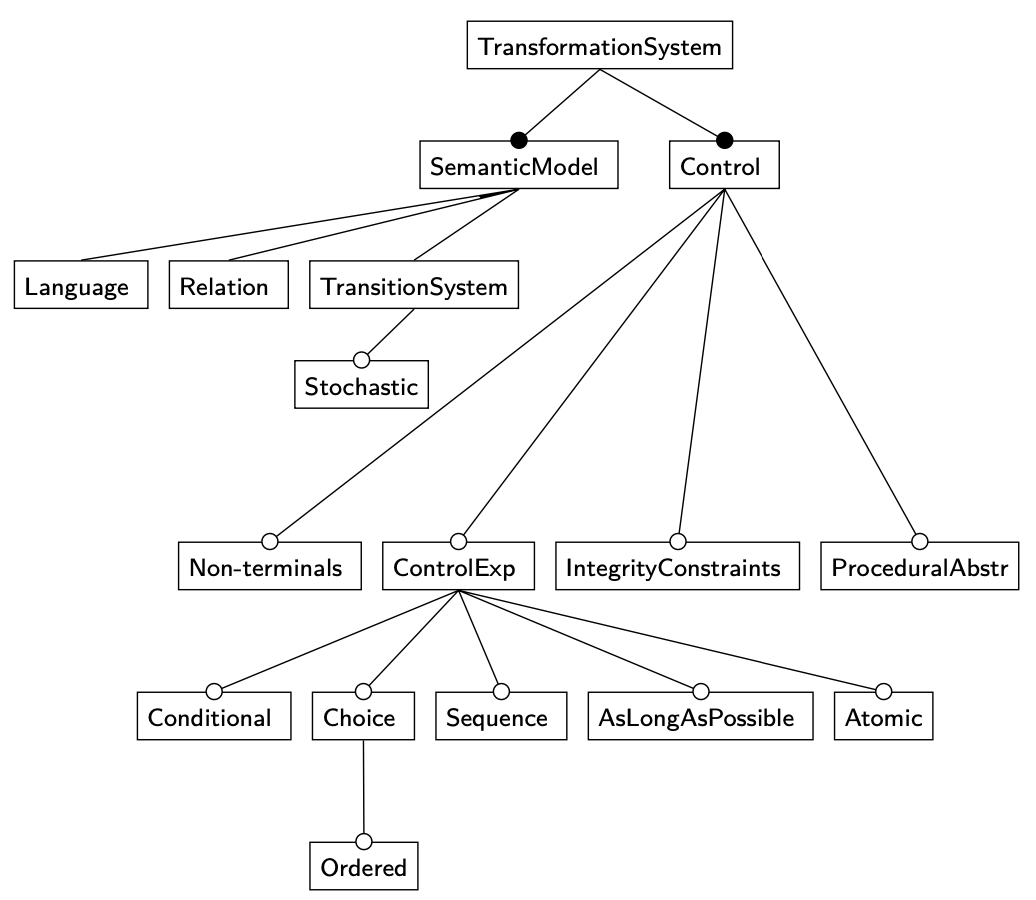
I. General strategies for control
- Unordered rules, but control via constraints / maintain program state ‘in the graph’
- Directed graph of rewrite rules
- No control of matches
- No complex control flow

- General program with
rewriteprimatives- No explicit control of matches
- Program language syntax

We want a graphical language for control flow + one which lets us say “use this match”.
II. AlgebraicRewriting
AlgebraicRewriting.jl is a library for graph rewriting written in Julia.
- Part of the AlgebraicJulia ecosystem
- Open source packages implementing computational CT / concrete applications.
- General computer algebra features for working in a variety of categories
- Emphasis and special support for the category of \(\mathsf{C}\)-Sets
AlgebraicRewriting supports:
- DPO, SPO, SqPO, Conegation, and PBPO+ rewriting
- Rewriting with attributes (e.g.
Int,Tuple{String, Float64}) - Application conditions (e.g. PAC, NAC, arbitrary commutative diagram constraints)
- Automated morphism search and incremental homomorphism search
- Automated functorial migration of rewrite rules between different schemas
- Enumeration of partial overlaps between graphs / \(\mathsf{C}\)-Sets
Installation is easy: just download Julia
II. Catlab basics review
- Declaring \(\mathsf{C}\)-Sets
- Manually, via
@acset - Via custom functions, e.g.
cycle_graph - Via (co)limits
- Manually, via
- Declaring morphisms between \(\mathsf{C}\)-Sets
- Manually, by specifying each component (e.g.
V=[2,3], E=[1]) - Via automated search + constraints, (e.g.
monic=true)
- Manually, by specifying each component (e.g.
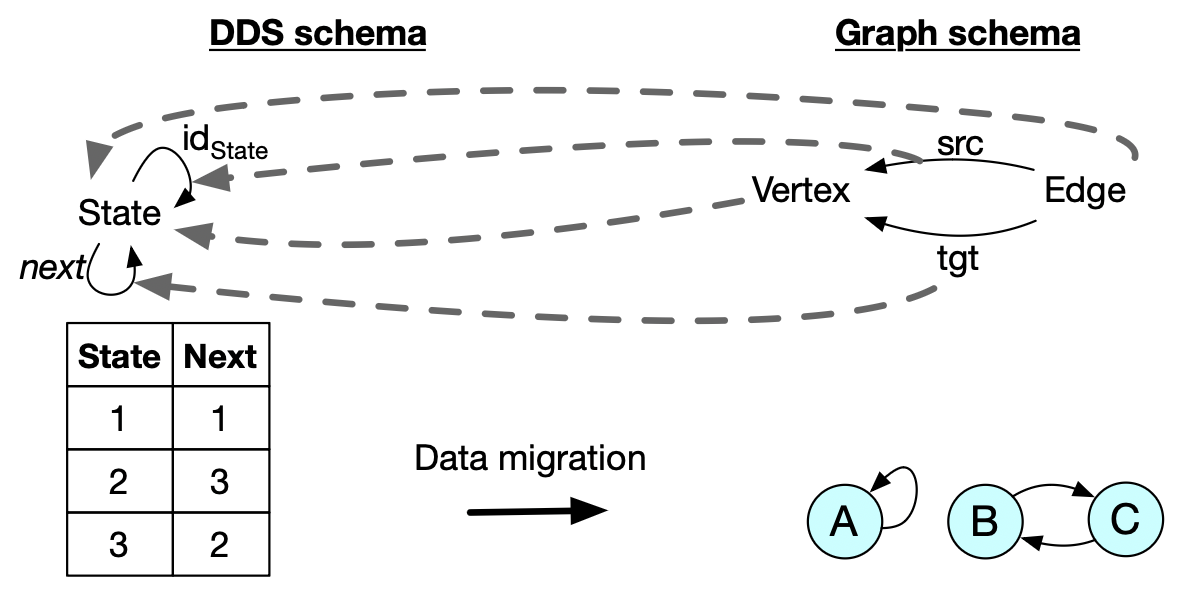
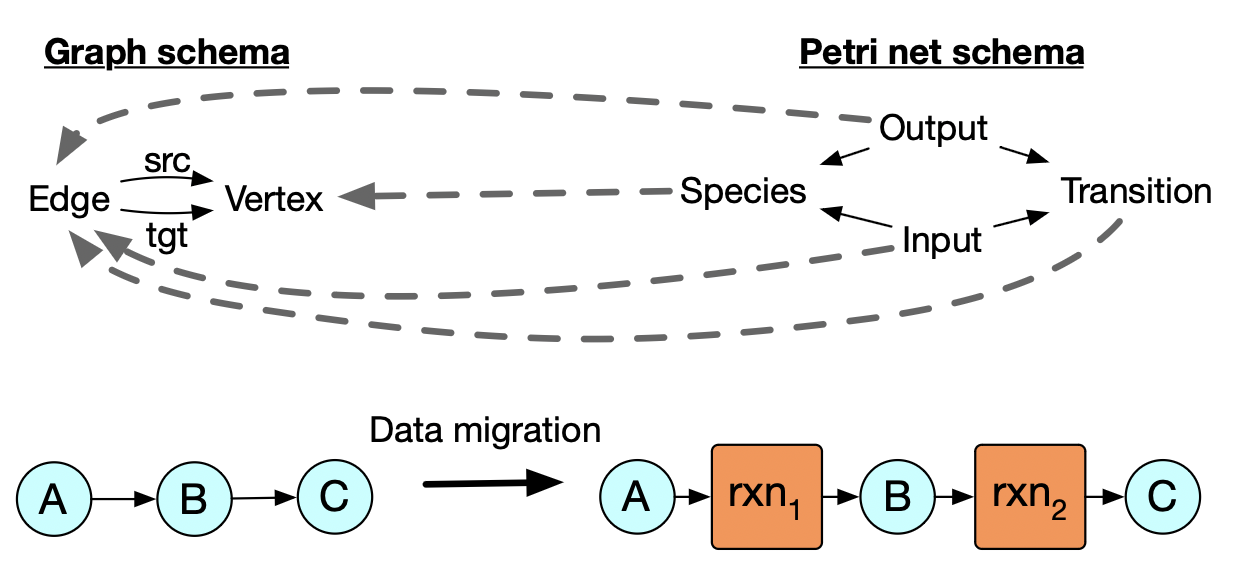
- CSet schemas (ACSet schemas)
- DDS, Graph, Petri Net (ChemicalRxn)
- Data migration:
- Functor between schemas presents transformation process on instances
- DDS to Graph, Graph to Petri Net
II. AlgebraicRewriting basics
AlgebraicRewriting introduces the Rule data structure:
zero = Graph(0)
edge = path_graph(Graph, 2)
del_edge = Rule{:SPO}(homomorphism(zero, edge), # L <- I
id(zero); # I -> R
monic=true # constraints on the match morphisms
ac=[PAC(...), NAC(...)] # feed in morphisms L -> P, L -> N
)
rewrite(del_edge, G) # result of applying an arbitrary match
L_to_G = homomorphism(edge, G) # pick a specific match
rewrite_match(del_edge, L_to_G) # rewrite with a specific match
res = rewrite_match_maps(del_edge, L_to_G) # return the entire derivation diagramAttributed \(\mathsf{C}\)-Sets (ACSets) can have concrete attribute values or variables (AttrVars).
- We can manipute the concrete variables with custom code
L = @acset WeightedGraph{Float64} begin
V=2; E=2; Weight=2; src=[1,1]; tgt=[2,2];
weight=[AttrVar(1), AttrVar(2)]
end
I = WeightedGraph{Float64}(2)
R = @acset WeightedGraph{Float64} begin
V=2; E=1; Weight=1; src=1; tgt=2;
weight=[AttrVar(1)]
end
l = homomorphism(I,L; monic=true)
r = homomorphism(I,R; monic=true)
merge_multiply = Rule(l, r; monic=[:E],
expr=Dict(:Weight=>[(w1, w2) -> w1*w2]))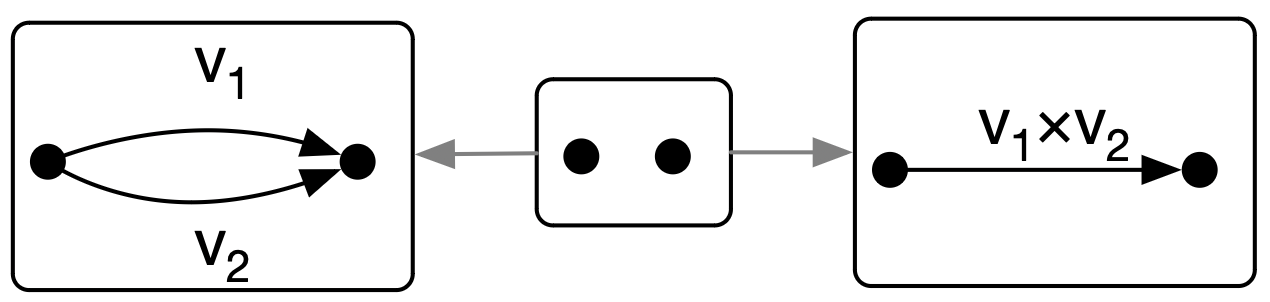
III. Rewrite programs: SMCs
Symmetric monoidal categories are a desirable structure for one’s syntax to have:
- Can be graphically depicted
- Can serve as the syntax for varying semantics

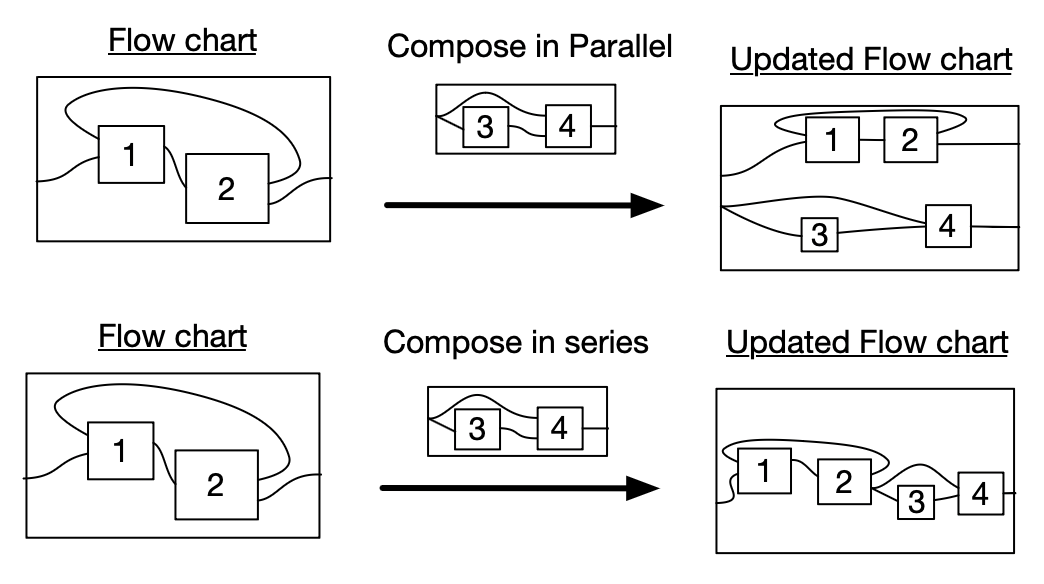
III. Rewrite programs: SMC composition
Symmetric monoidal categories are a desirable structure for one’s syntax to have:
- Can be graphically depicted
- Can serve as the syntax for varying semantics
- Can be composed in parallel or in series
- With further traced structure, we can have loops.
III. Rewrite programs: SMC substitution
Symmetric monoidal categories are a desirable structure for one’s syntax to have:
- Can be graphically depicted
- Can serve as the syntax for varying semantics
- Can be composed in parallel or in series
- With further traced structure, we can have loops.
- Can be operadically substituted
Graphical language of function composition
\(\mathbf{Set_*}\) has the required traced monoidal structure (using coproducts for \(\otimes\)).
Thus we can use this language to talk about composition of functions.
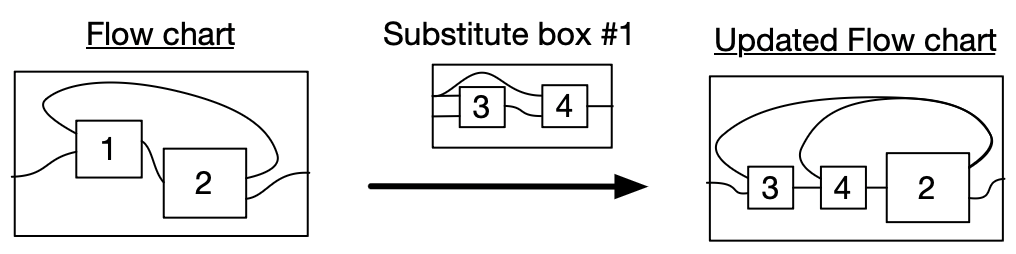
Think of rewrite rule add_loop as a function1 \(Grph \rightarrow Grph + Grph\):

Add a loop to a vertex. If none exists, then add a vertex, then give it a loop.
Graphical language of function composition
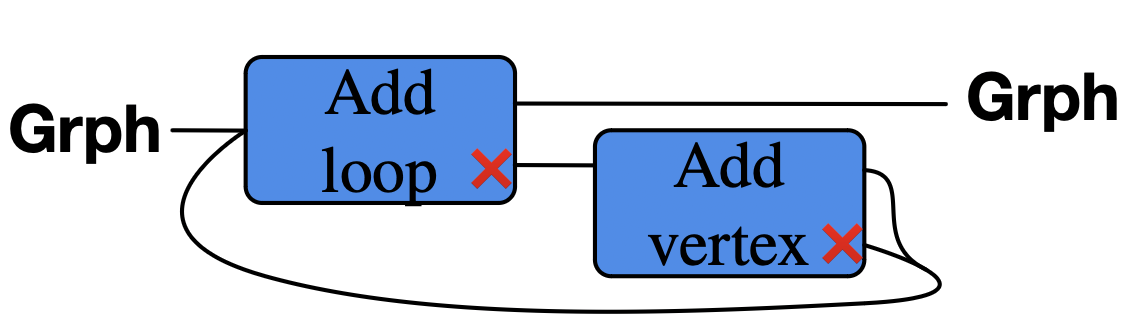
New primitive type of box for control flow:
- Can only redirect its input, not modify it
- \(A \xrightarrow{f} n \times A\) for \(n \in \mathbb{N}\) such that \(f\cdot \pi_i = id_A\)
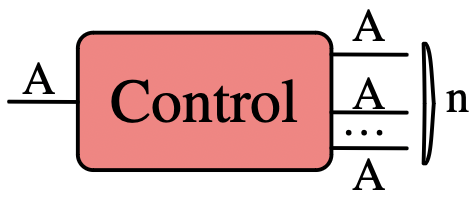
Remove edges, until we have a DAG
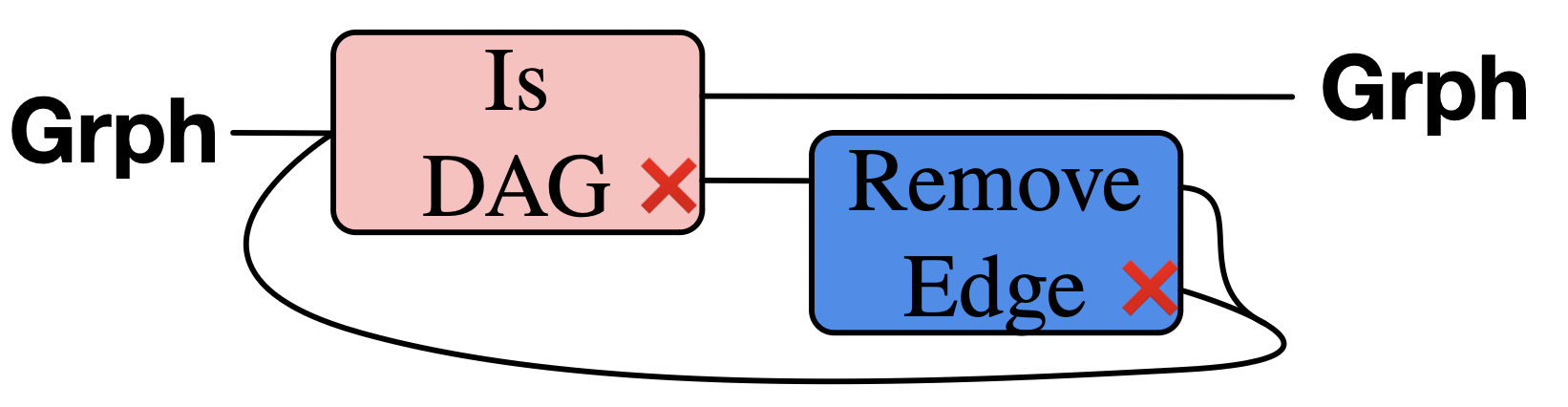
Remove an edge, distinguish between cases of empty result or not

Graphical language of dynamic function composition
Mealy machines (or dynamic functions) seem to form a symmetric monoidal category.1
\[Hom_{\mathbf{Meal}}(A:Set,B:Set) := \left\{\left(S : \mathsf{Set},\ s_0 : S,\ \phi\colon A\times S\to S\times B\right)\right\}\]
- We allow
Controlboxes to have nontrivial state.
A control flow box which decrements its internal state each time it is entered:

A box which behaves like Add Loop the first three times it is used, then like Delete Vertex:

Control of matches via a notion of ‘agent’
Our wires are labeled with “agent shapes”. These are \(\mathsf{C}\)-Sets.
- Set of possible values associated with a wire is the set of morphisms \(A \rightarrow G\) for some \(\mathsf{C}\)-Set \(G\).


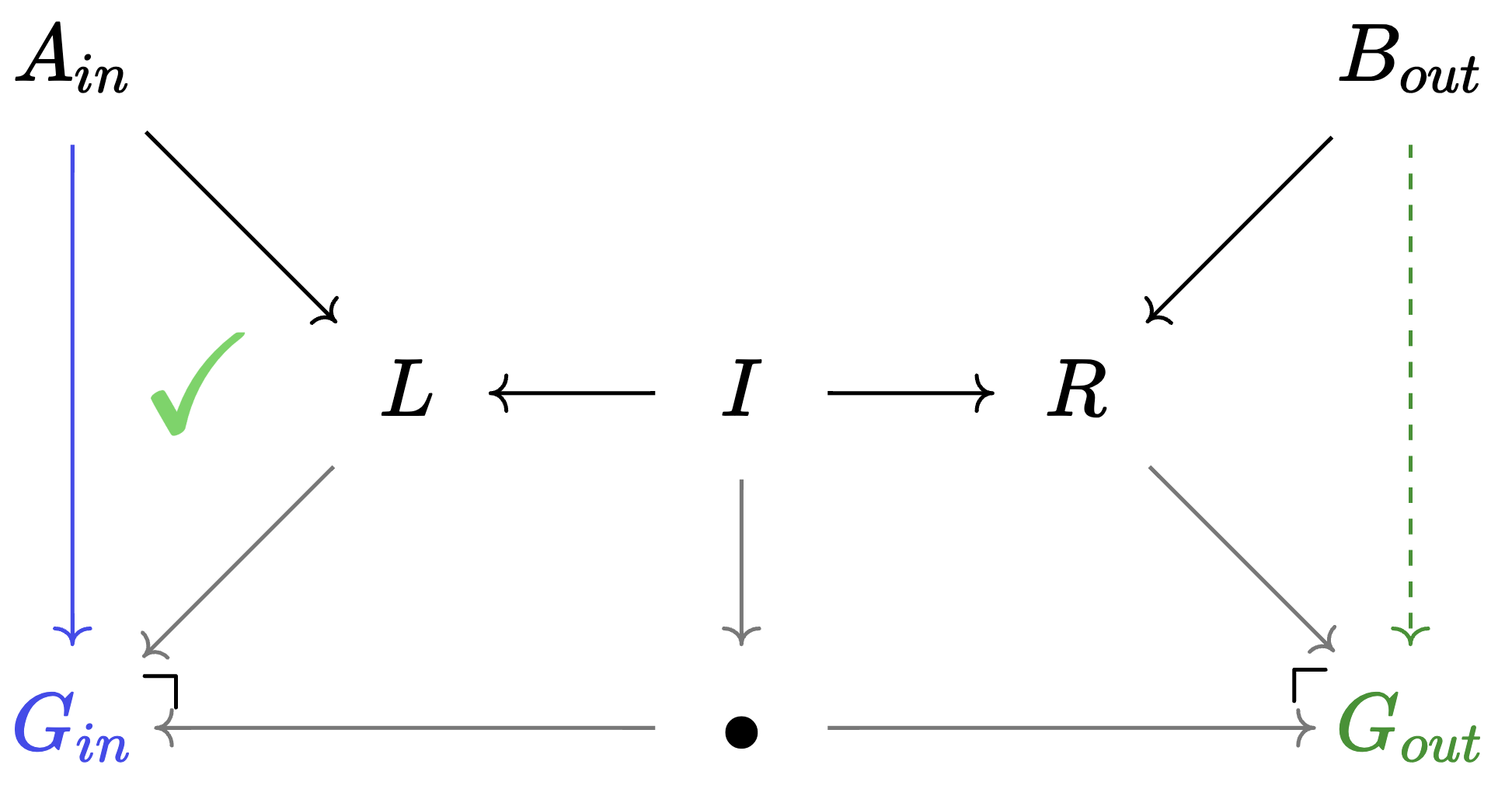
- Crucial difference between adding a loop to some vertex vs adding a loop to this vertex.
- Gradient between two extremes:
- determinism (\(A = L\))
- nondeterminism (\(A = \varnothing\))
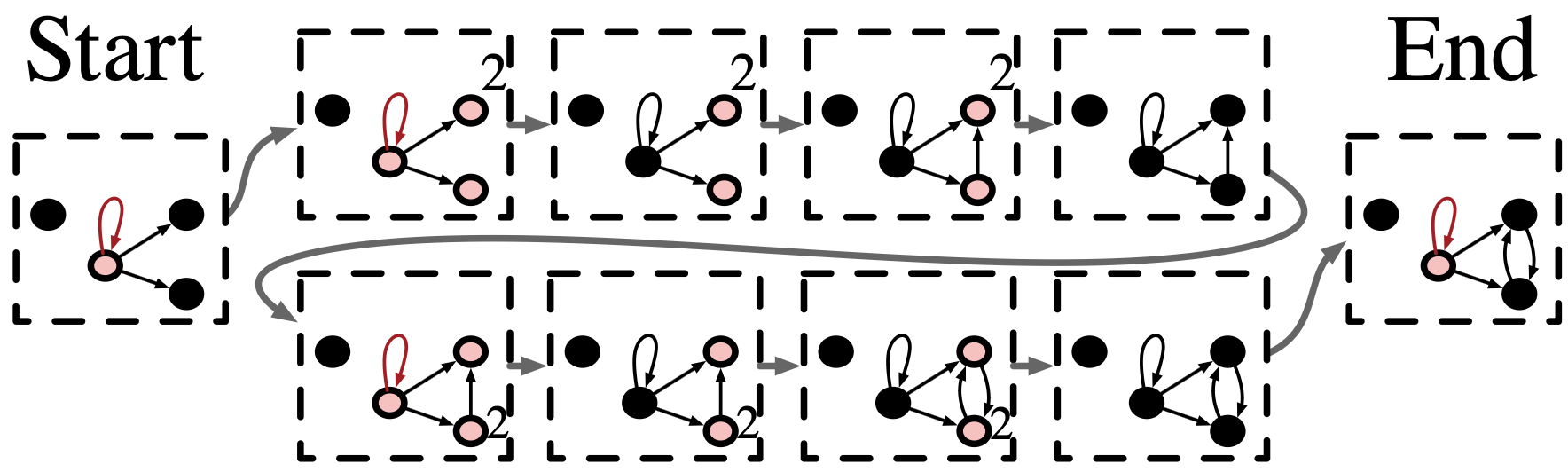
Example of rewriting with control of matches

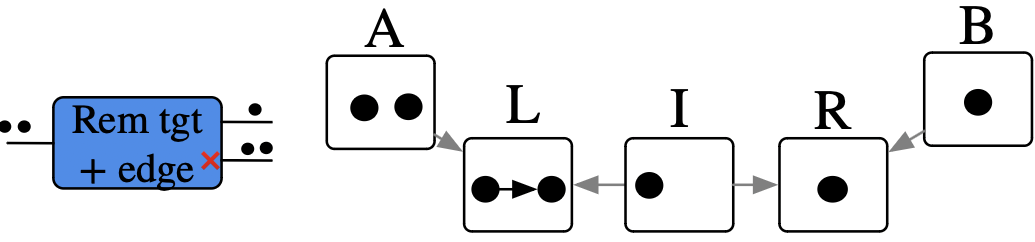
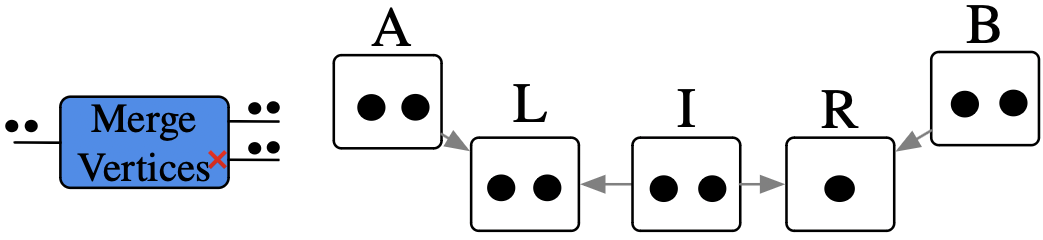

Example: Binary DAGs
Suppose we want to classify binary DAGs1

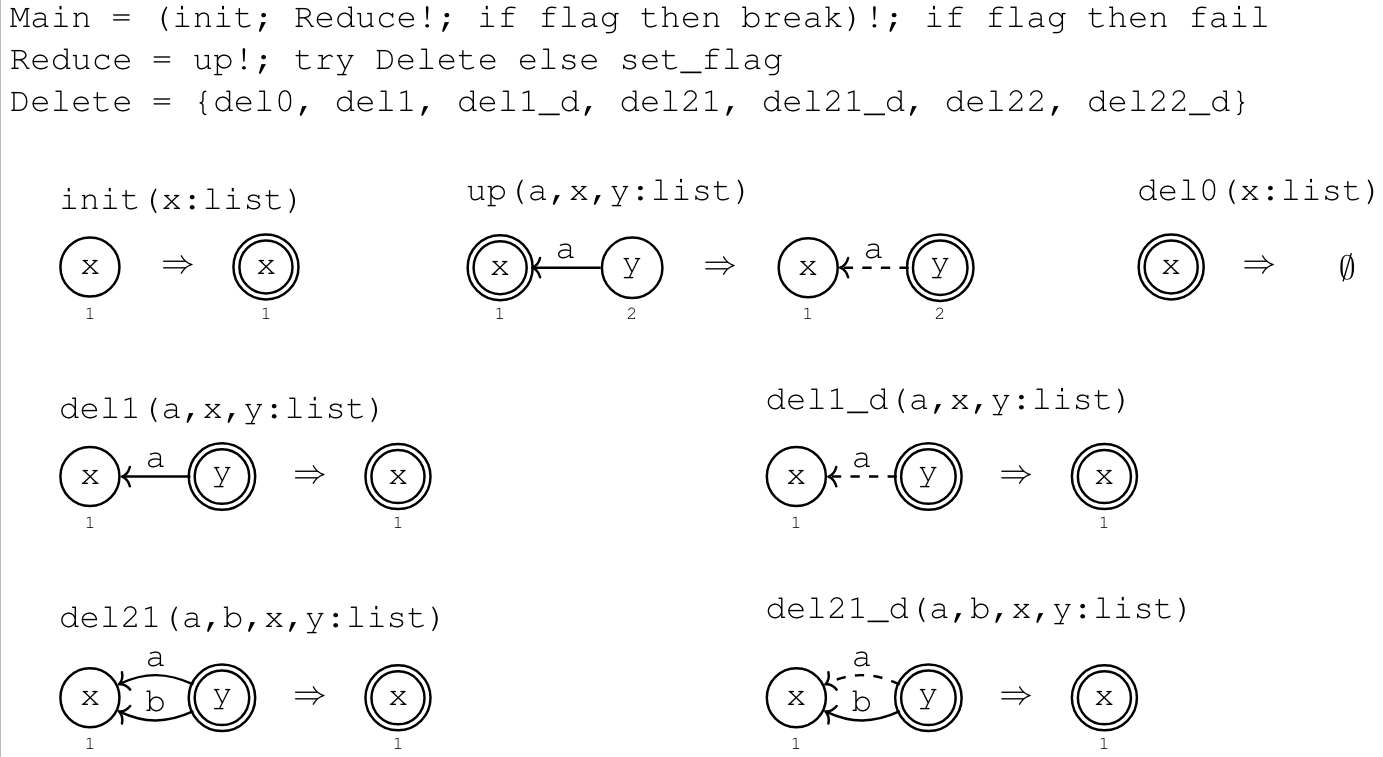
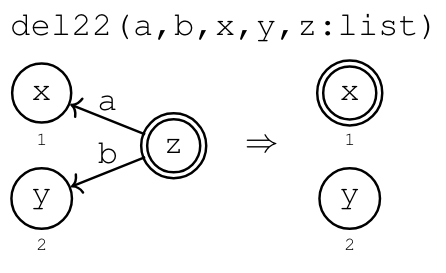
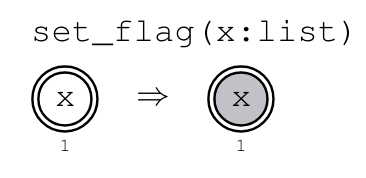
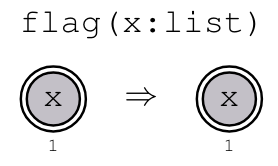
Example: Binary DAGs
Rewrite program in a category with schema \(\boxed{V \leftleftarrows E \leftarrow Seen}\)

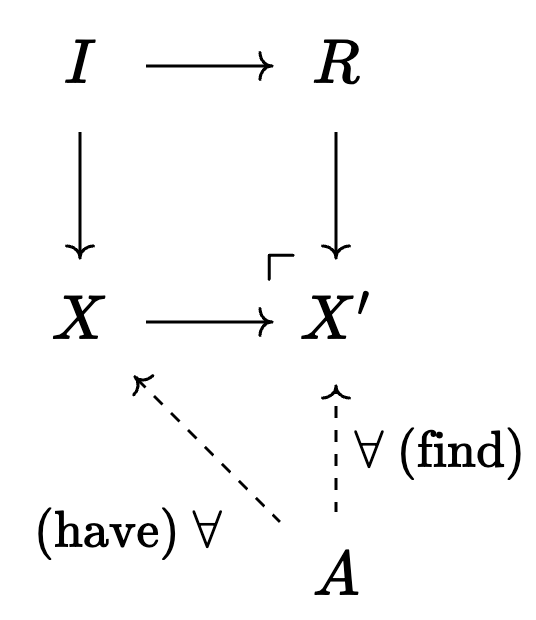
Weaken: switching to less specific agents
Weaken is specified by a morphism \(Hom_{C\mathsf{Set}}(A,B)\).

- It converts \(B\)-agents to \(A\)-agents without changing the state of the world.
- It acts upon an agent via precomposition.
- Equivalent to a rewrite rule with \(A_{in} = L = I = R\)
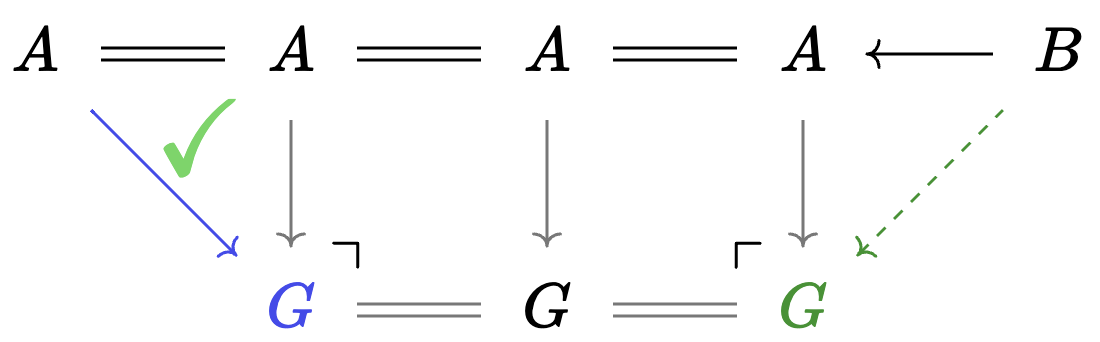
Weaken: switching to less specific agents
Weaken is specified by a morphism \(Hom_{C\mathsf{Set}}(A,B)\).

- It converts \(B\)-agents to \(A\)-agents without changing the state of the world.
- It acts upon an agent via precomposition.
- Equivalent to a rewrite rule with \(A_{in} = L = I = R\)
We can always weaken with the initial object:
- Rewriting with initial agent is forgoing any explicit control of matches.
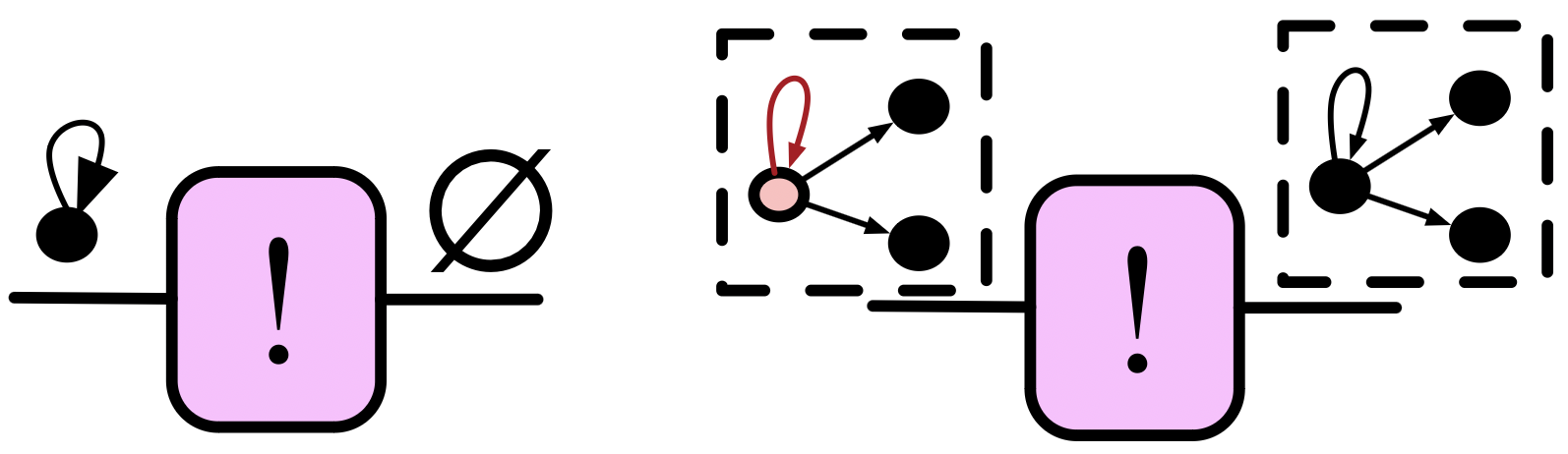
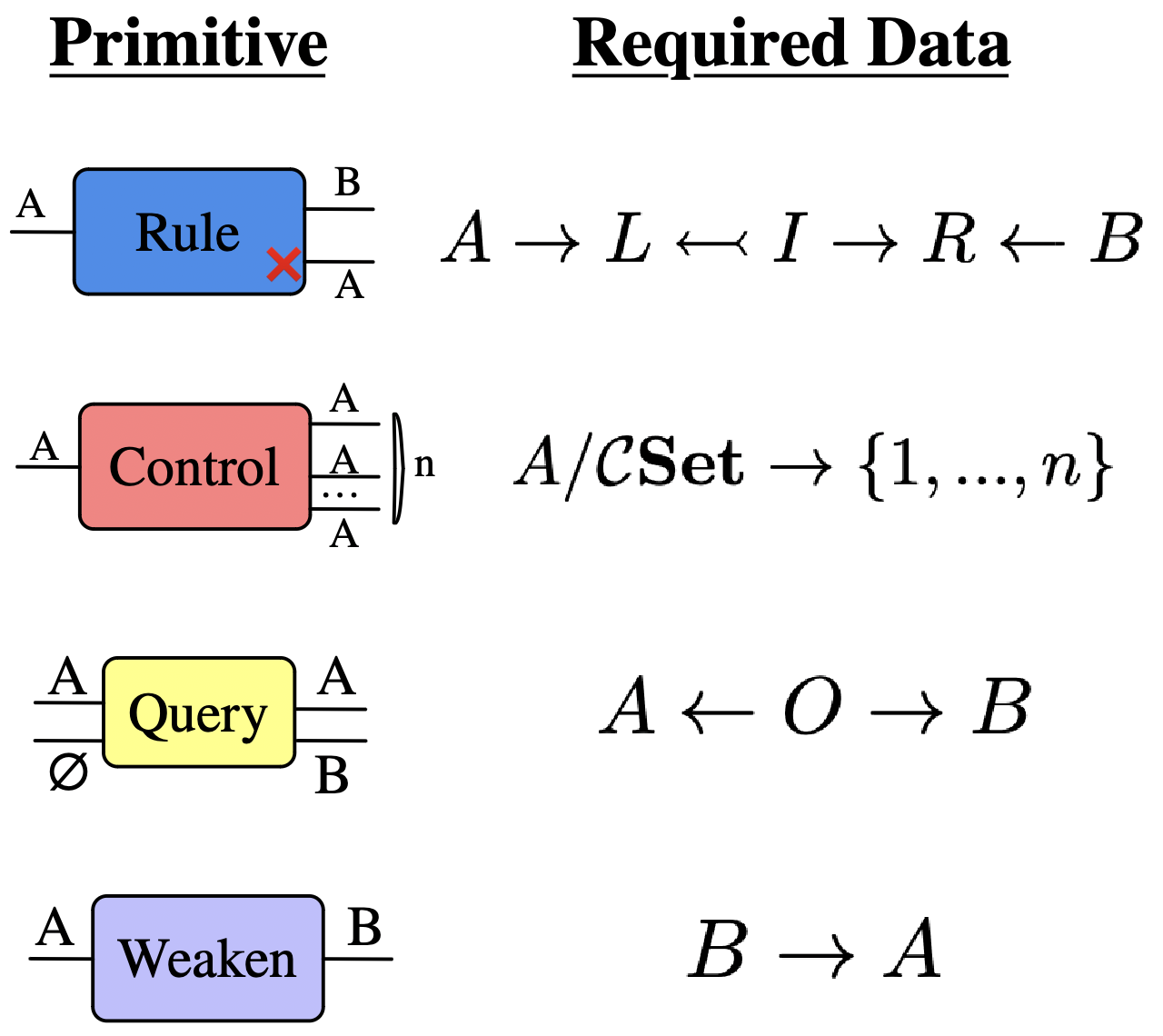
The Query primitive: more specific agents
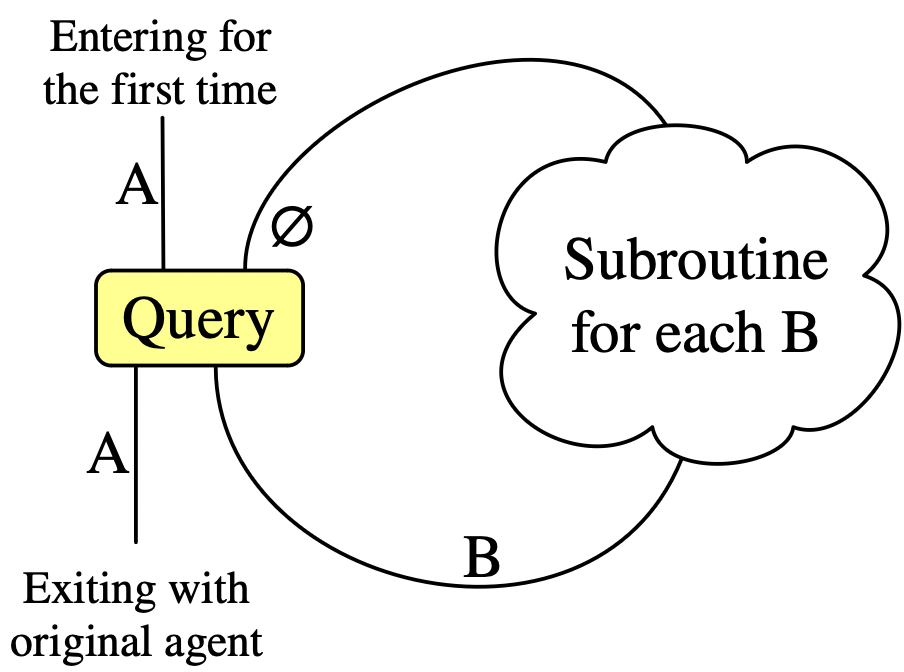
Required data: 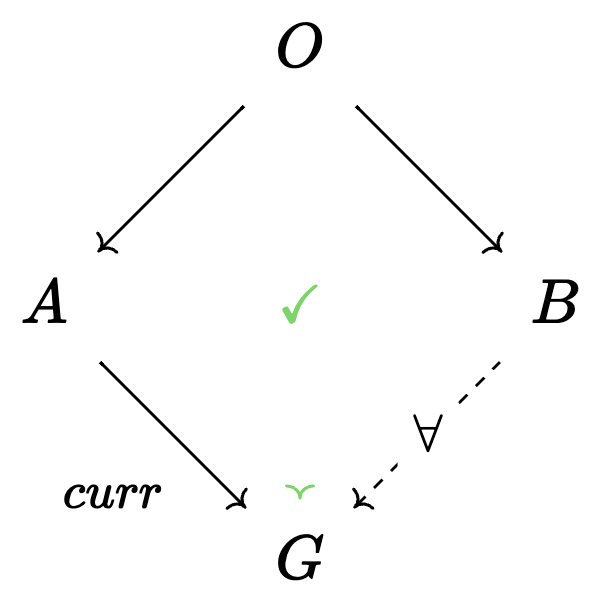
Example:
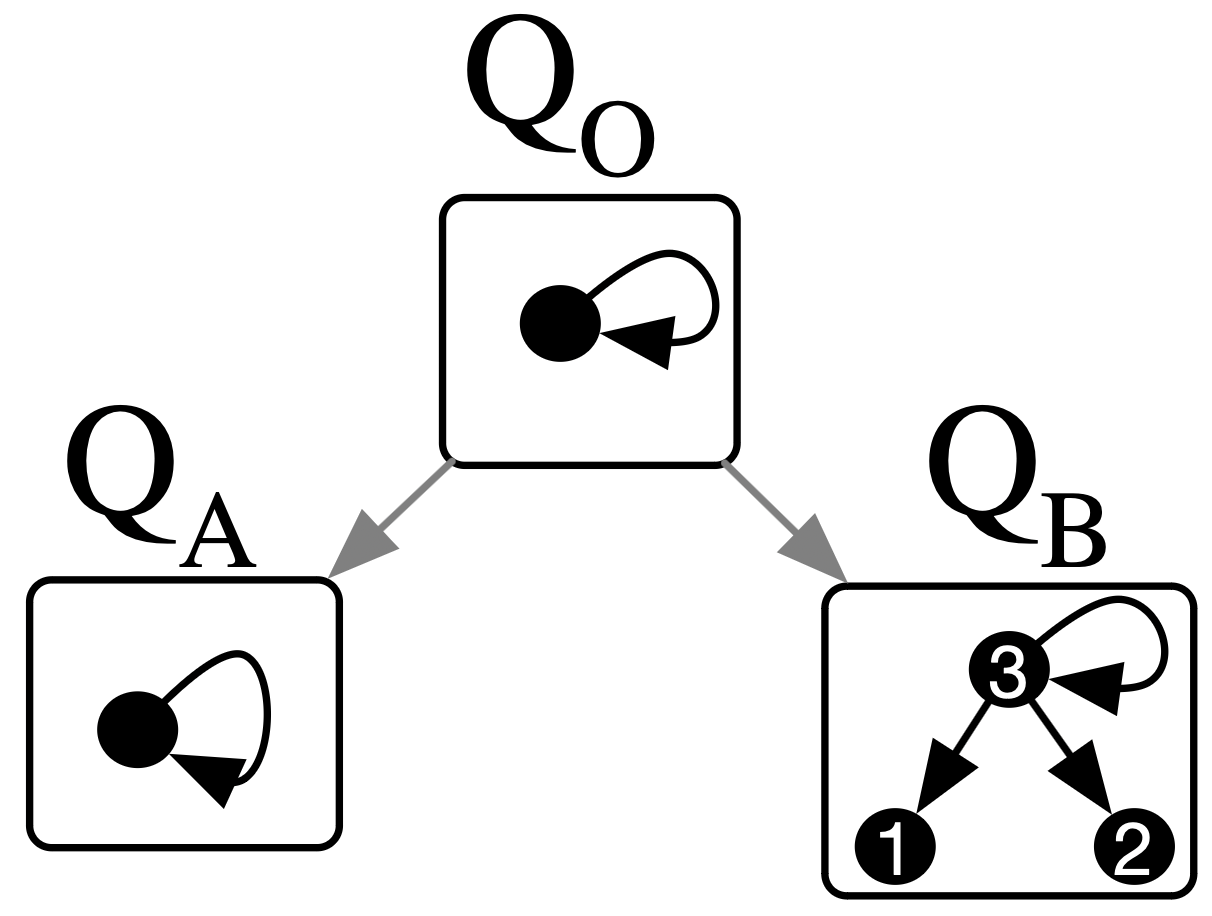
Fully connect all the outneighbor vertices of some distinguished loop
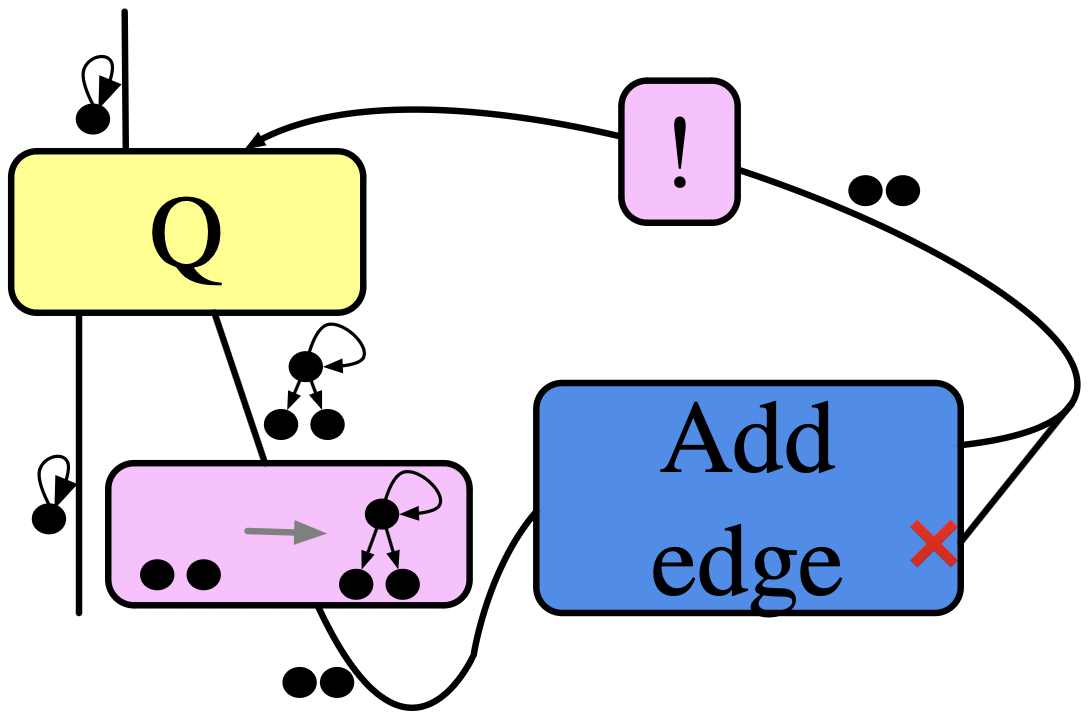
Summary of rewriting programs
- Mealy machine primitives composed via directed wiring diagrams
- Wires represent sets of morphisms \(A \rightarrow X\) for a fixed \(A\)
- Changes are only performed by
Rule - Shifting ‘agent’ focus performed by
QueryandWeaken
Implementing ABMs via agent-based programs
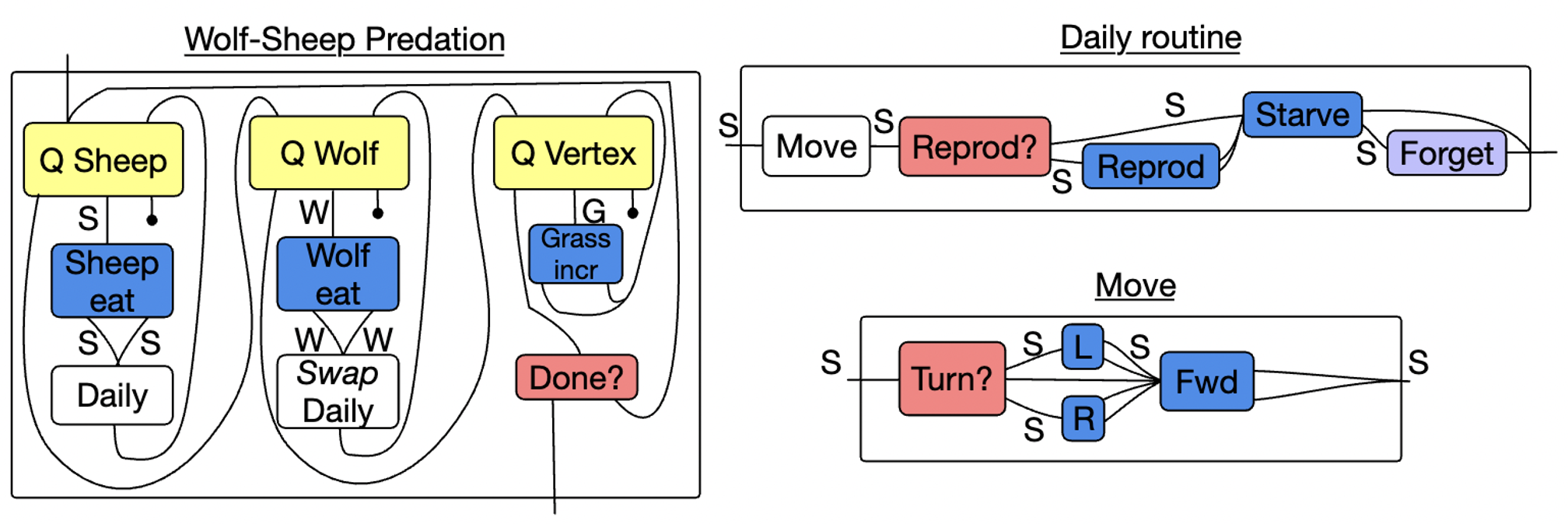

Why are these rewriting ‘programs’ rather than ‘models’?
These feel less like programs compared to (equivalent) syntax like:
- Can be graphically depicted
- Can be composed in parallel or in series
- Can be operadically substituted
- Can easily vary semantics
Nevertheless, this is not suited for agent-based modeling
- Control flow fundamentally imperative rather than declarative.
- To understand a diagram, you must run a simulation in your head.
- No built-in notion of time
- Always a linear sequence of events
- No capability for concurrency
- No capability for continuous time events
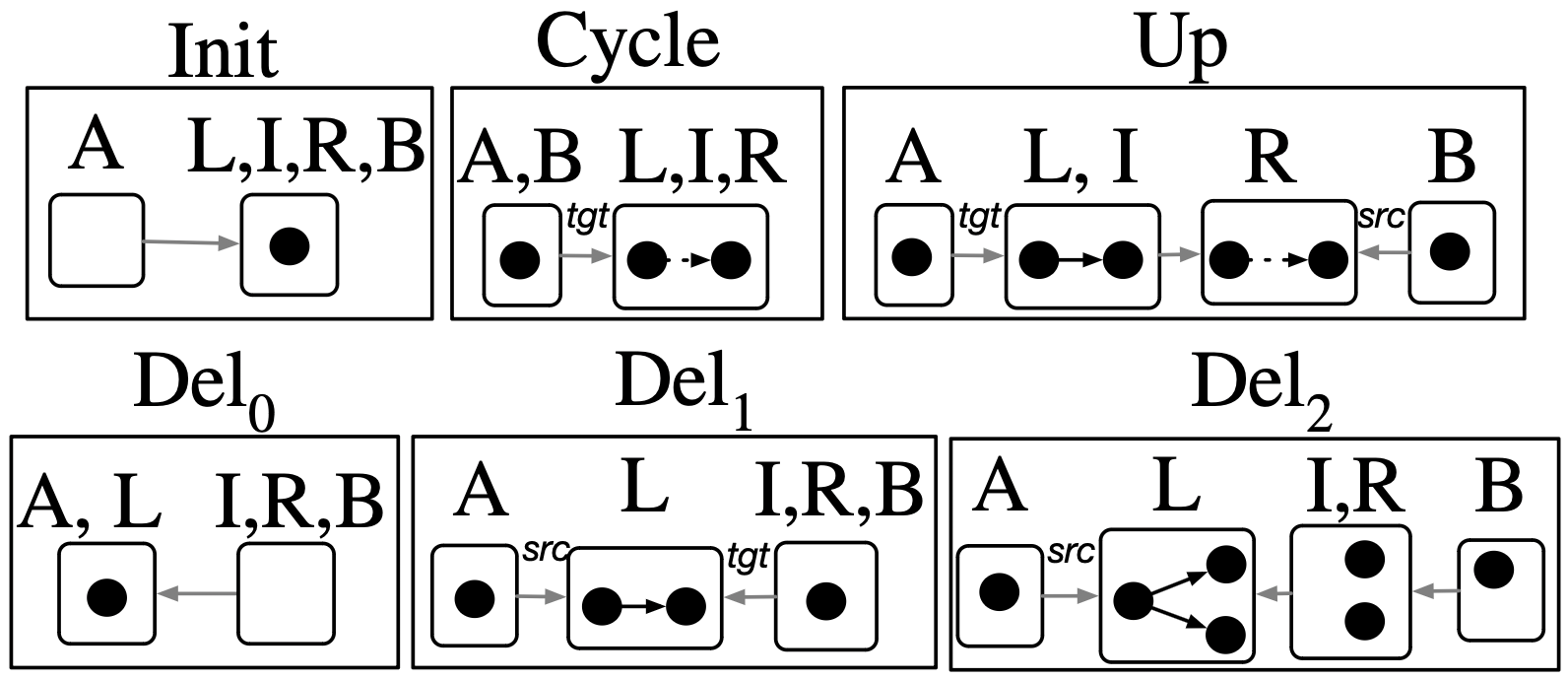
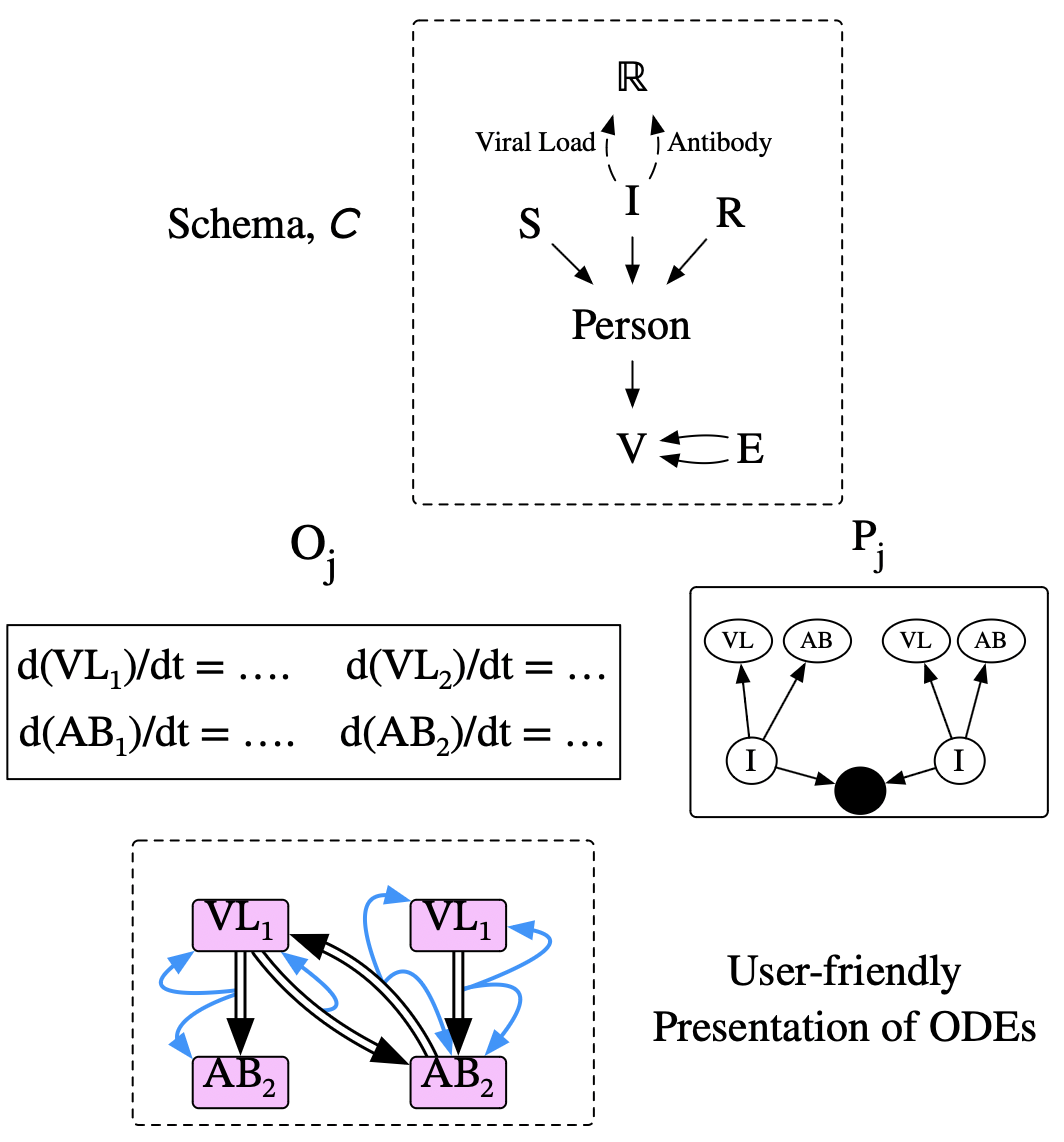
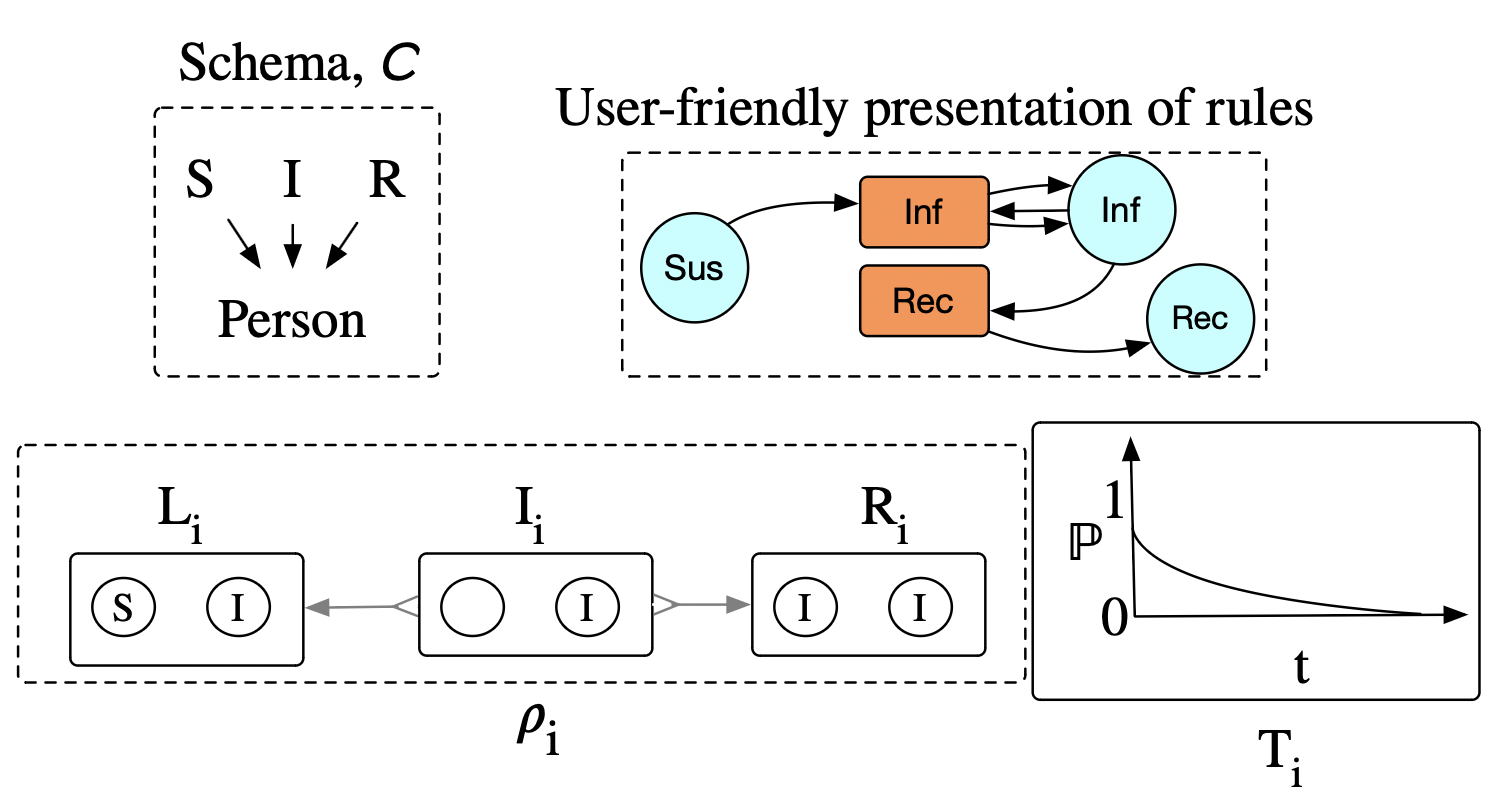
IV: Agent-based modeling1
These models are continuous time with discrete events and continuous dynamics.
To first order, an ABM is:
- A schema: possible world states are ACSet instances
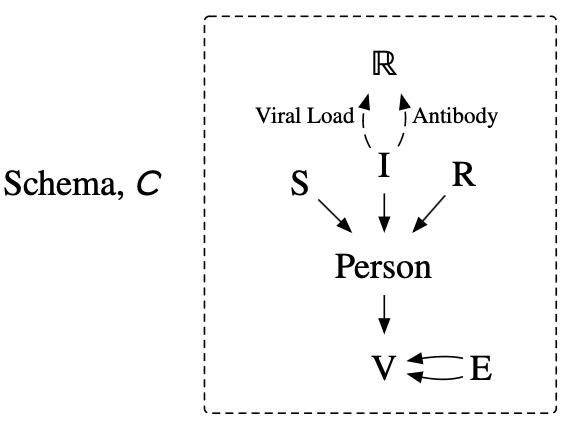
IV: Agent-based modeling1
These models are continuous time with discrete events and continuous dynamics.
To first order, an ABM is:
- A schema: possible world states are ACSet instances
- A collection of rewrite rules, \(\rho_i :: (L_i \leftarrowtail I_i \rightarrow R_i)\rightarrow \mathbf{ACSet}\)
- An associated collection of ‘timers’ \(T_i :: \mathsf{P}([0,\infty])\).
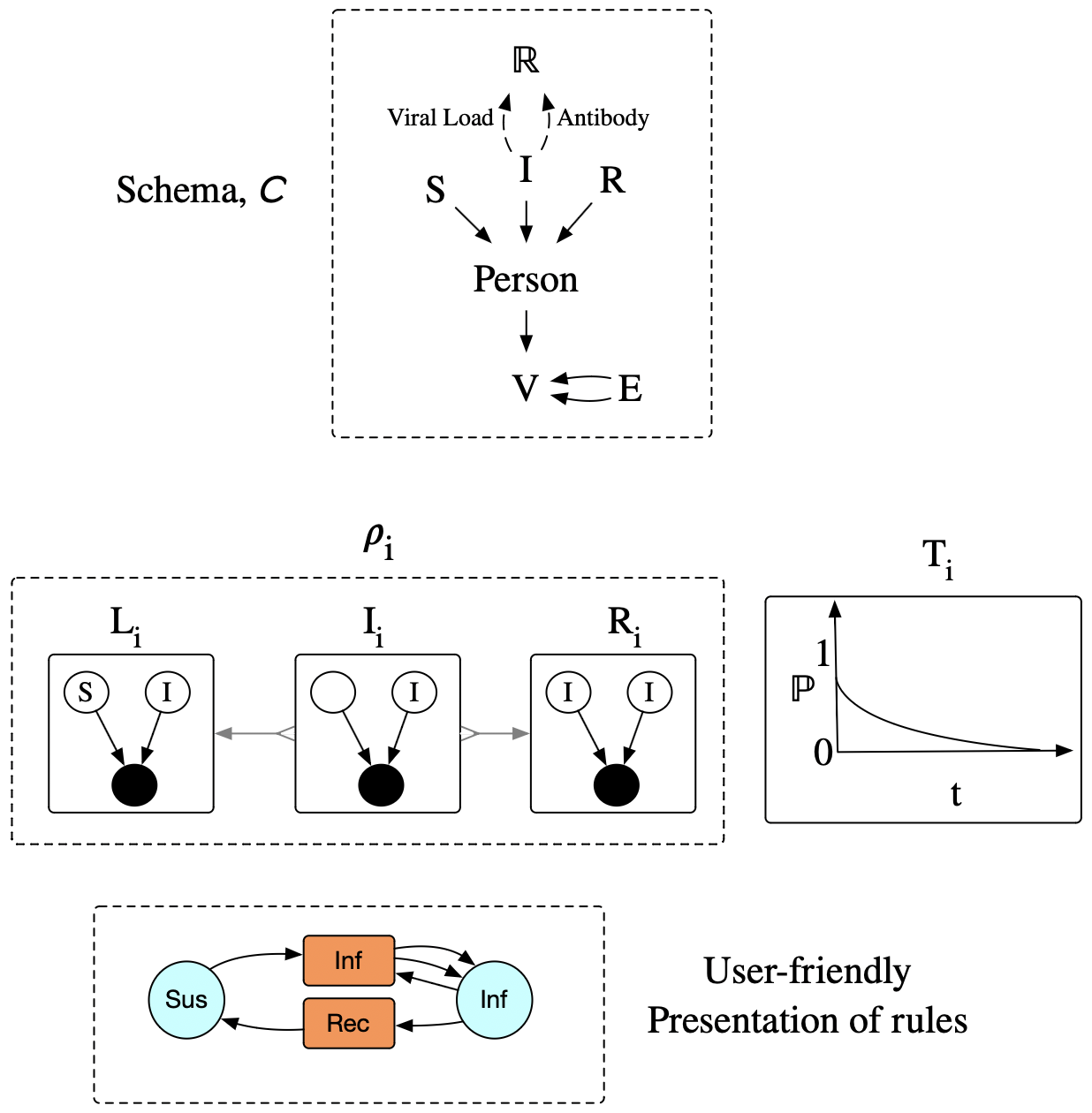
IV: Semi-Markovian ‘timers’
The probability measure captures a ‘residence time’:
- how long it takes to happen, conditional on nothing else happening first to remove it from that state.
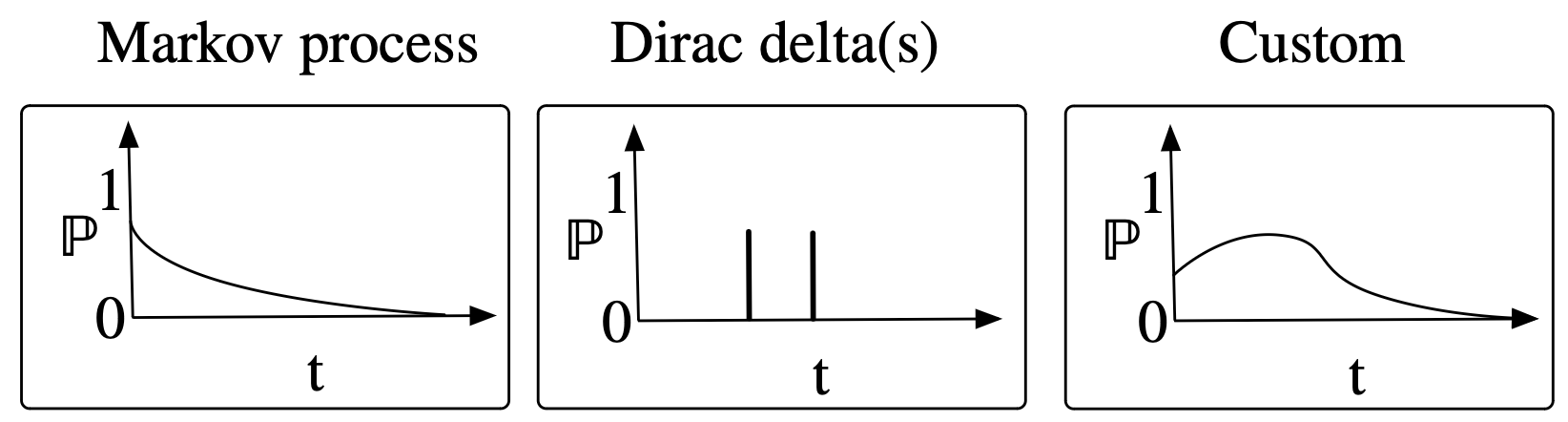
- “staying in a state” = “match persists” over time
E.g.

Generalization: these are parameterized by the state of the world:
- the probability of (\(S_i\), \(I_j\)) depends on the viral load of \(I_j\)
- the probability of \(I_j\) recovering depends on the total # of doctors
IV: Agent-based modeling1
These models are continuous time with discrete events and continuous dynamics.
To first order, an ABM is:
- A schema: possible world states are ACSet instances
- A collection of rewrite rules, \(\rho_i :: (L_i \leftarrowtail I_i \rightarrow R_i)\rightarrow \mathbf{ACSet}\)
- An associated collection of ‘timers’ \(T_i :: \mathsf{P}([0,\infty])\).
- A collection of continuous dynamics, given by ODEs \(O_j\)
- An associated collection of patterns, \(P_j :: \operatorname{Ob}(\mathbf{ACSet})\).
- Partial functions from \(P_j\) variables to \(O_j\) variables.
Example: Game of Life
@present SchLifeGraph <: SchSymmetricGraph begin
Life::Ob; live::Hom(Life,V)
end
@acset_type LifeState(SchLifeGraph); # defines LifeState
# Helper functions / building blocks
#-----------------------------------
Cell = LifeState(1) # one vertex, nothing else
LiveCell = @acset LifeState begin V=1; Life=1; live=1 end
to_life = homomorphism(Cell, LiveCell);
living_neighbors(n::Int; alive=true)::ACSetTransformation = ...
# Rules
#------
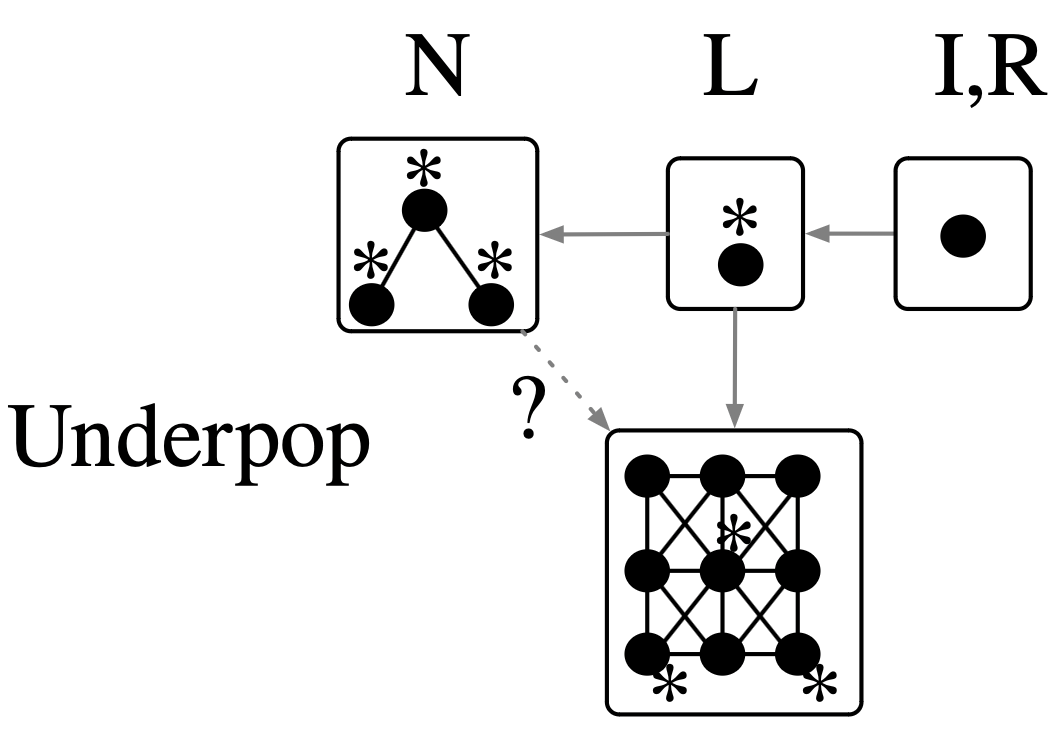
underpop = TickRule(:Underpop, to_life, id(Cell);
ac=[NAC(living_neighbors(2))]);
overpop = TickRule(:Overpop, to_life, id(Cell);
ac=[PAC(living_neighbors(4))]);
birth = TickRule(:Birth, id(Cell), to_life;
ac=[PAC(living_neighbors(3; alive=false)),
NAC(living_neighbors(4; alive=false)),
NAC(to_life)]); # doesn't apply if alive
GoL = ABM([underpop, overpop, birth]) # model is just the rules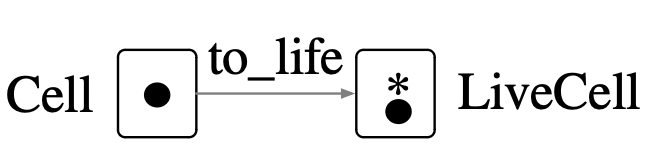
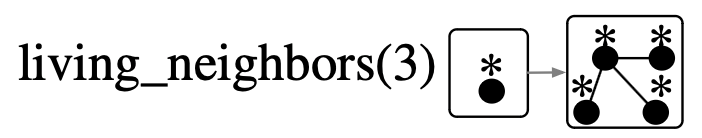
Example: Petri net token semantics
sir_pn = @acset LabelledPetriNet begin
S=3; sname=[:S,:I,:R]
T=2; tname=[:inf,:rec]
I=3; is=[1,2,2]; it=[1,1,2];
O=3; os=[2,2,3]; ot=[1,1,2]
end
# Create ABM by associating stochastic timers with each T
abm = ABM(sir_pn, (inf=ContinuousHazard(1000),
rec=ContinuousHazard(Weibull(30, 5)...)));
# Initial state
init = PetriNetCSet(sir_pn; S=95, I=5)
# Run the model
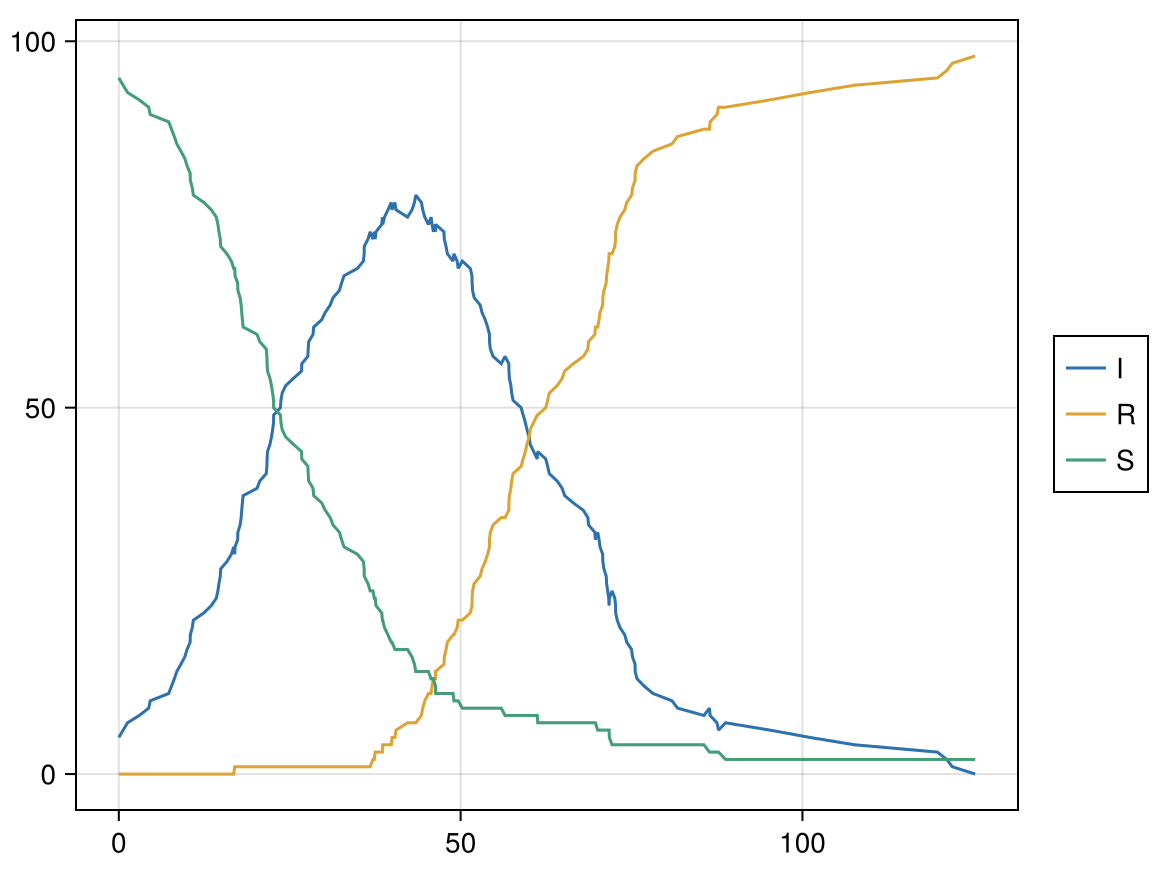
res = run!(abm, init; maxtime=2000);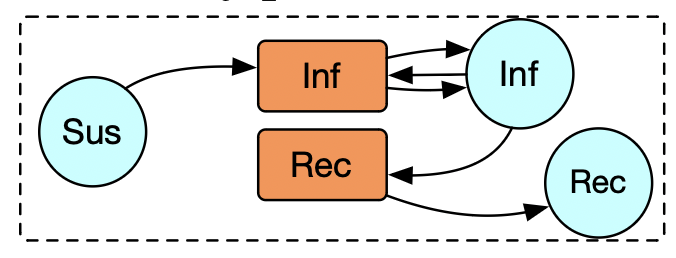
Performance: representable patterns
In certain circumstances, we don’t have to keep track of all the matches explicitly.
- We have a simple exponential (memoryless) probability distribution
- The pattern is a coproduct of representables (e.g. \(L = \bullet \oplus \bullet \rightarrow \bullet\))
In this case, rather than draw a timer for every \((S, I)\) pair with probability \(e^{-kt}\), we draw just one timer with probability \(e^{-k*(|S|*|I|)t}\), then randomly pick a match at firing time.
Performance: Incremental homomorphism search
For each overlap with \(R \setminus I\):
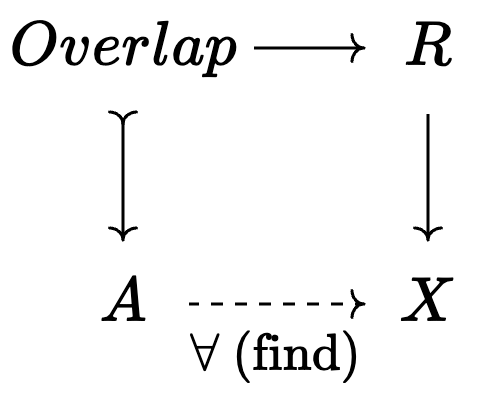
Synthesis of agent-based programs and models
One does not have to choose between ABP and ABM. In fact, we can use both:
- Generalize the earlier definition of ABM: pairs of ABP+timer
- Our previous formalism is a special case where all programs consist in just a single rule.
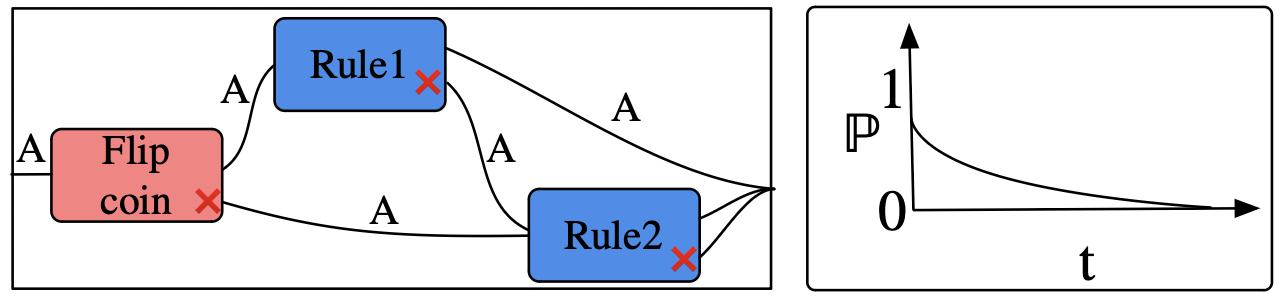
This lets us express things such as: after 5.0 s, something definitely happens, but which rule is applied depends on coin toss (or first one rule is tried, and a different is tried if that fails).
V: Conclusion
- AlgebraicRewriting is expressive, powerful, easy to install, easy to use.
- AlgebraicJulia is moving in a direction of factoring out our language-specific features, so that the same core can be instantiated in Python, Java, Rust, etc.
- Graphical rewrite programs built from
ControlFlow,Rewrite,Query, andWeaken- This syntax can be given a solid mathematical semantics.
- Control flow + language for control over matches
- Agent-based models can be constructed declaratively
- A clear separation of schema, actions, and timing.
- We could associate timers with entire programs, rather than individual rules.
- This can be used for cellular automata, epidemiology, operations research
- Libraries: Catlab.jl, AlgebraicRewriting.jl, AlgebraicABMs.jl
- Blog posts: Agent-based programming, Coupling ODEs to ACSets
- Papers: AlgebraicRewriting.jl, Rewriting programs
- Models: Wolf-Sheep Program, GoL Program, GoL ABM, Petri Net ABM, Pertussis ABM
Thanks for your attention
About the Topos Institute

Mission: to shape technology for public benefit by advancing sciences of connection and integration.
Three pillars of our work, from theory to practice to social impact:
- Collaborative modeling in science and engineering
- Collective intelligence, including theories of systems and interaction
- Research ethics
- Physics simulations (PDEs) with Decapodes.jl
- Reaction networks with AlgebraicPetri.jl
- Epidemiological modeling with StockFlow.jl
- Agent-based modeling with AlgebraicRewriting.jl
- Interactive GUIs with Semagrams
- Vision: topos.institute
- Research: topos.site
- Blog: topos.site/blog
Topos Institute is a 501(c)(3) non-profit organization
II. Catlab basics preview
- Declaring \(\mathsf{C}\)-Sets
- Manually, via
@acset - Via custom functions, e.g.
cycle_graph - Via (co)limits
- Manually, via
- Declaring morphisms between \(\mathsf{C}\)-Sets
- Manually, by specifying each component (e.g.
V=[2,3], E=[1]) - Via automated search + constraints, (e.g.
monic=true)
- Manually, by specifying each component (e.g.
- CSet schemas (ACSet schemas)
- DDS, Graph, Petri Net (ChemicalRxn)
- Data migration:
- Functor between schemas presents transformation process on instances
- DDS to Graph, Graph to Petri Net
II. Catlab basics: category of directed multigraphs
II. Catlab basics: attributes
We are not limited to working with the category of directed multigraphs. Attributed C-Sets (ACSets) can have concrete attribute values in the ambient programming language.
@present SchChemicalRxn(FreeSchema) begin
(Atom, Bond, Molecule)::Ob
# Functional relationships
bond_atom::Hom(Bond, Atom)
bond_pair::Hom(Bond, Bond)
molecule::Hom(Atom, Molecule)
# Equations
bond_pair ⋅ bond_pair == id(Bond)
# Data types and attributes
(N, ℝ)::AttrType
atomic_number::Attr(Atom, N)
stoichiometry::Attr(Molecule, ℝ)
endII. Catlab basics: attributes
We are not limited to working with the category of directed multigraphs. Attributed C-Sets (ACSets) can have concrete attribute values in the ambient programming language.
@present SchChemicalRxn(FreeSchema) begin
(Atom, Bond, Molecule)::Ob
# Functional relationships
bond_atom::Hom(Bond, Atom)
bond_pair::Hom(Bond, Bond)
molecule::Hom(Atom, Molecule)
# Equations
bond_pair ⋅ bond_pair == id(Bond)
# Data types and attributes
(N, ℝ)::AttrType
atomic_number::Attr(Atom, N)
stoichiometry::Attr(Molecule, ℝ)
end@acset_type ChemicalRxn(SchChemicalRxn){Int, Float64}
O2 = @acset ChemicalRxn begin
Atom=2; Bond=4; Molecule=1
bond_atom=[1,2,1,2]; bond_pair=[2,1,4,3]
atomic_number=[8, 8]; molecule=[1,1]
stoichiometry=[1.0]
end
# Get a symmetry of the molecule: swap the atoms
sigma = homomorphism(O2, O2; initial=(Atom=[2,1],))
II. Catlab basics: more schemas
II. Catlab basics: data migration
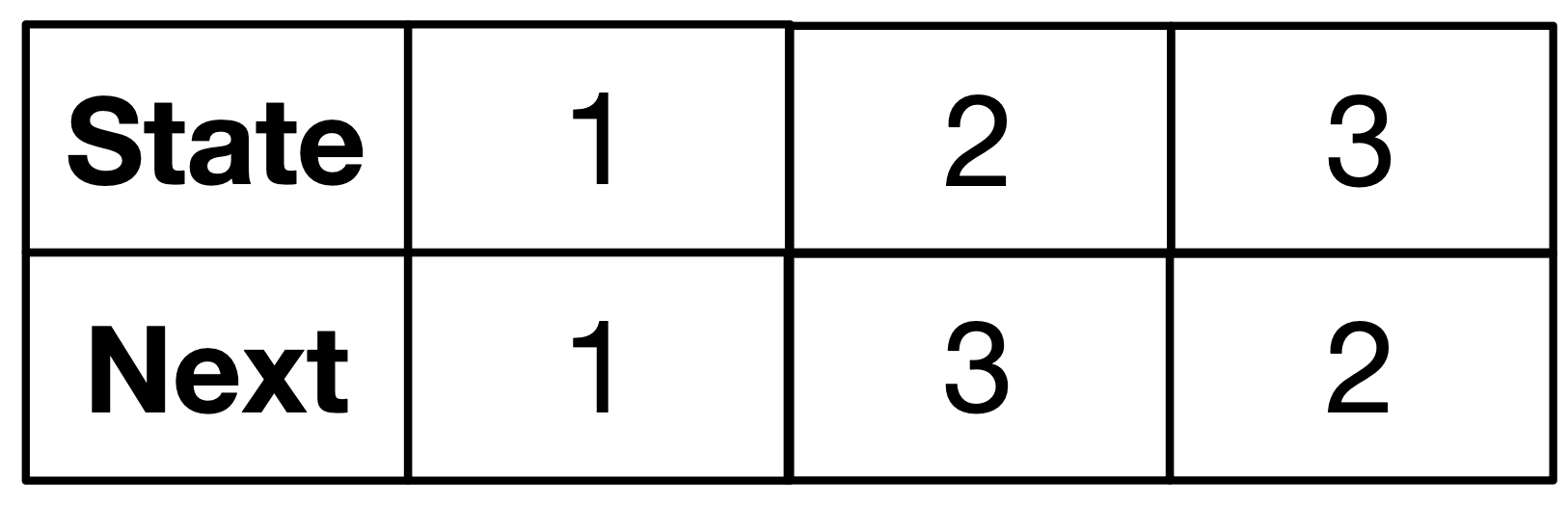
DDS as a special kind of directed graph:
- each vertex has a “next” edge.
Graphs as a special kind of Petri net
- each edge is a 1-input, 1-output transition.