. . .
Next, I want to move onto Petri nets, which are a way of looking at bipartite graphs, where we interpret one of the vertex types, call them transitions, as hyperedges which have multiple inputs and multiple outputs. This is especially relevant to modeling epidemiology or supply chains or chemical reaction networks. It might be of interest that these can also be thought of as instances of a certain database schema, which means if we understand the basic structure of databases then we do not have to write much Petri-net-specific code at all.
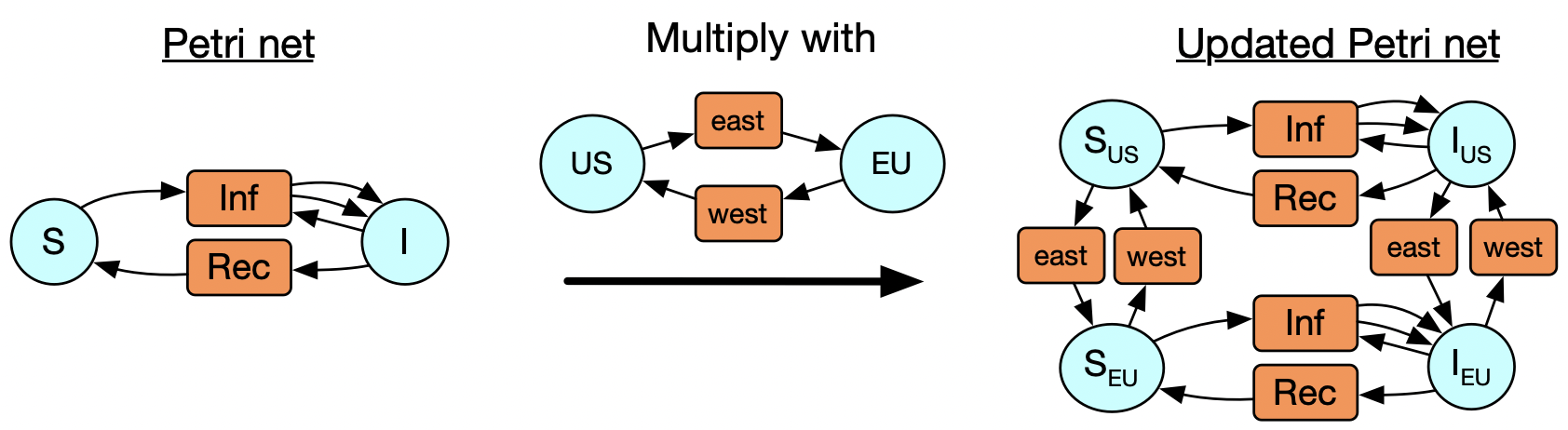
Let’s start with the example of a world where there are susceptible and infected people, and it takes a susceptible + an infected person to make two infected people, and the infected people can recover spontaneously too. This is just a specification of what sorts of transitions are possible without saying anything about their rates. There are two particular ways of taking a positive real number weight for each transition and obtaining a dynamical system: one of which is to create an ODE using mass-action kinetics (like in chemistry) and another is to do a stochastic simulation where you keep track of individual tokens living inside all of the blue circles and randomly trigger the transitions to fire. (…)
I’m going to talk about a new problem, but should first mention that the gluing problem from before is still relevant to petri nets. We can do the exact same AlgebraicJulia solution from before (flip back to previous slide) if we wanted without having to write any new code, whereas our two code-based solutions from before would have to be rewritten from scratch, something that feels very similar but still is completely different because these data structures look pretty different. But to keep things interesting let me talk about a different kind of abstraction reuse problem in the Petri net scenario.
Now consider that we may realize that, after running our simulation, that we should have made a distinction: what we thought was one homogenous group of susceptible people is better modeled by two US and a European populations, and likewise for infected people. It’s possible for someone to travel by plane and move from one of these populations to the other, too. We could express this itself as a Petri net with two states and two transitions, and only might we realize that our new model is really the multiplication of our starting Petri net with another one, in a sense that can be made precise. It would be nice to be able to declare that and be done with it, but first I’ll walk you through how we’d to do this in the old paradigm.