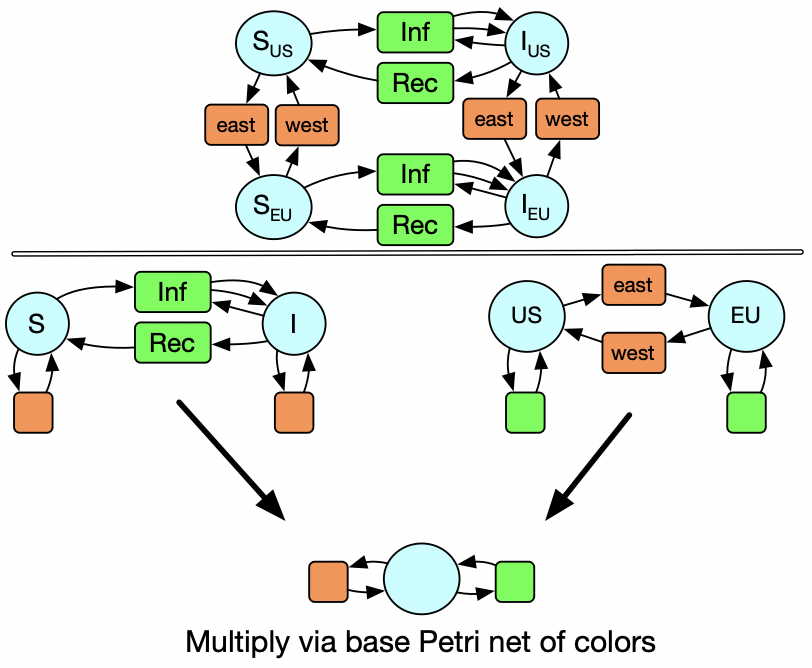
Just as we had a generalized notion of gluing things together, which did not rely on the internals of what we were gluing but just how they were externally related to each other (their relation to the boundary we glued them along), there is a general notion of multiplying things together. The essence of multiply is looking for pairs of things, so if you have two of one thing and three of another, there are six possible pairs where you can take one from each. We can slightly generalize this where we don’t take all pairs but rather just pairs of “similar things”. The coloring of the circles and boxes here shows that, if we think of there being one kind of species but two kinds of transitions, then it’s the case that we can multiply these two Petri nets to do exactly what this upper right function is doing. But our mathematical understanding of what this multiply function is really doing allows us to understand it in a very general way - so we can use this same code to multiply graphs or other database-based data structures.