Outline

I. Future of software engineering

II. Mini examples of the future paradigm

III. Intuition for how structural mathematics works

Note: it’s not feasible to cover category theory at a technical level in such a short talk, rather I want to show what you can do with it. So I’ll be avoiding jargon whenever possible, including the phrase “category theory” itself! Rather, we should just think of category theory as ‘the mathematics of structure’: something that makes precise our intuitions about structure in a way that allows us to actually compute things.

Stages of development for software engineering

We solve problems one at a time, as they come.

This starts feeling repetitive.

. . .

Abstractions act as a solution to an entire class of problems.

This feels repetitive insofar as we feel the problem classes are related.

Common abstractions are things like functions / datatypes / scripts in our language.

. . .

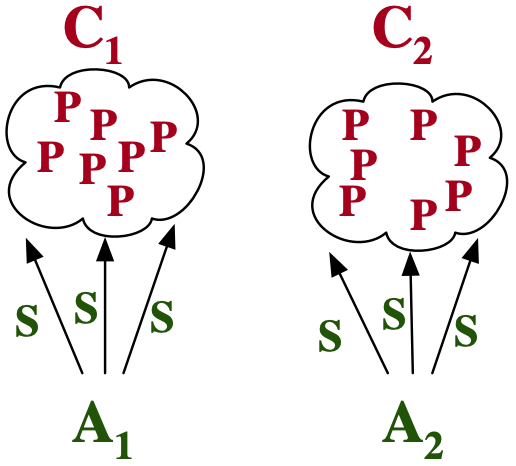
We migrate abstractions to allow them to address changes in problem specification.

Future paradigm: mathematically-principled + automatic migration

Understand structure of the abstraction + implementation + the relationship between them.

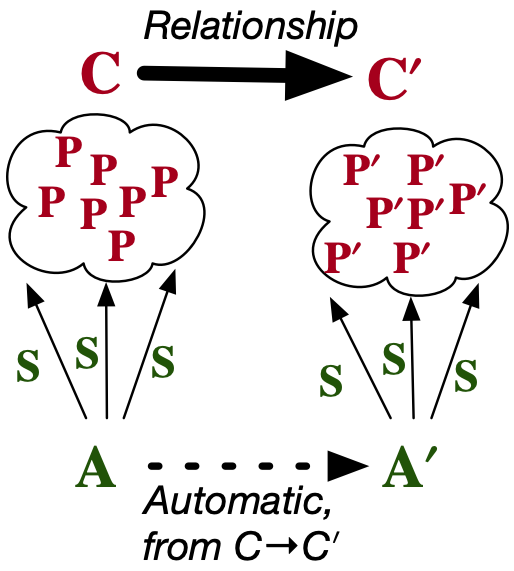
This slide summarizes everything I want to talk about today. (Stage 1)

(…) (Stage 2)

(…) (Stage 3)

There will be lots of examples illustrating how we can move from Stage 2 to 3 when we use abstractions that we understand well. I’ll try to clearly show what’s going on for toy examples and then (at the end) Evan will showcase some real, practical examples at a high level.

Three examples of abstractions

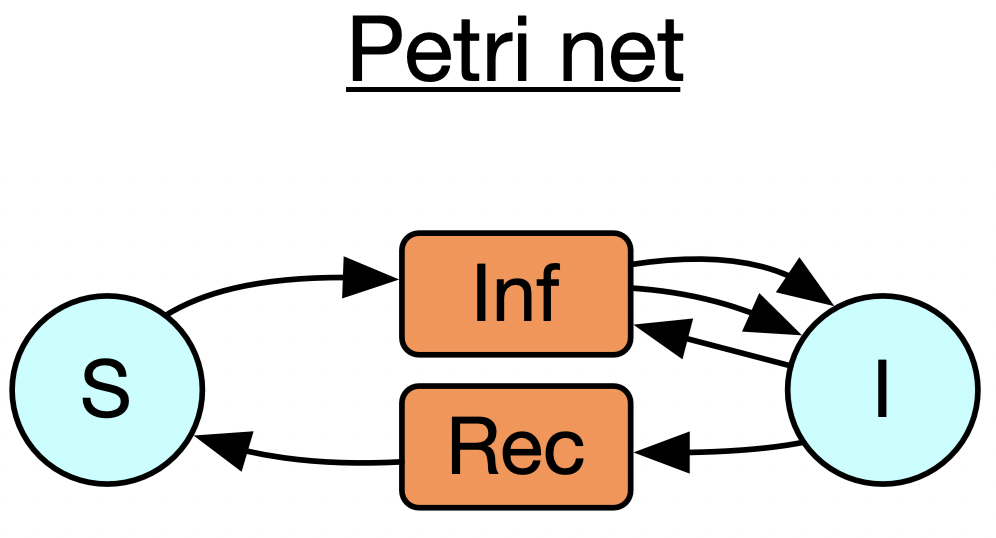
In this section of the talk: I’ll make reference to three specific types of abstractions which I’ll introduce one at a time. These are databases (here I’m just showing a particular toy database schema), Petri nets (also called bipartite graphs), and wiring diagrams

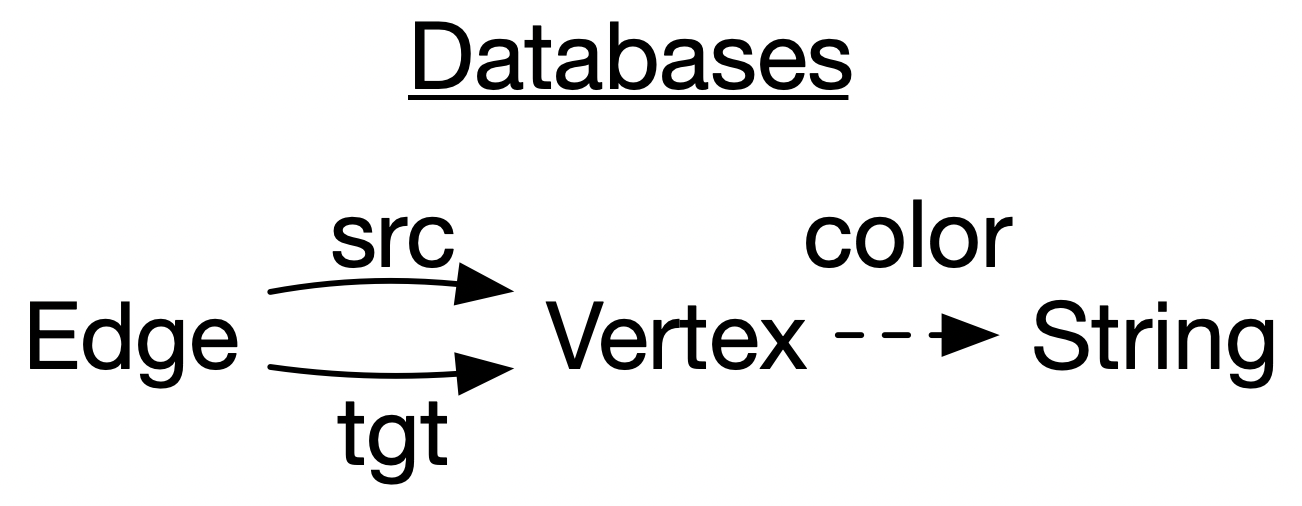
Abstraction: databases

CREATE SCHEMA COLORGRAPH;
CREATE TABLE VERT (ID PRIMARY KEY, COLOR VARCHAR);
CREATE TABLE EDGE (ID PRIMARY KEY, 
                   FOREIGN KEY TGT REFERENCES VERT(ID),
                   FOREIGN KEY SRC REFERENCES VERT(ID));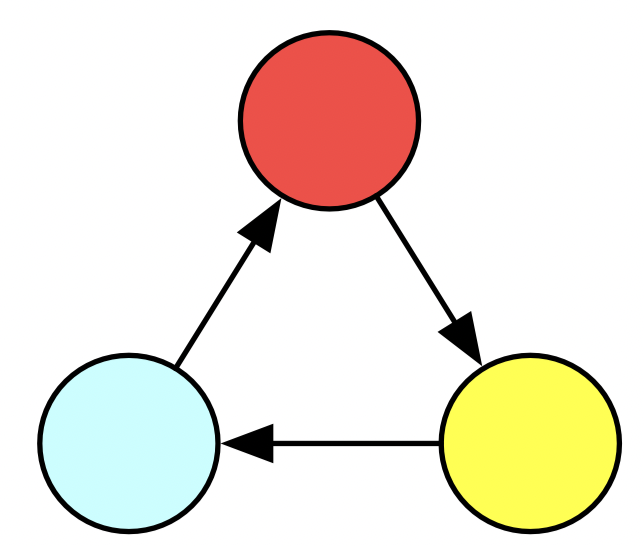

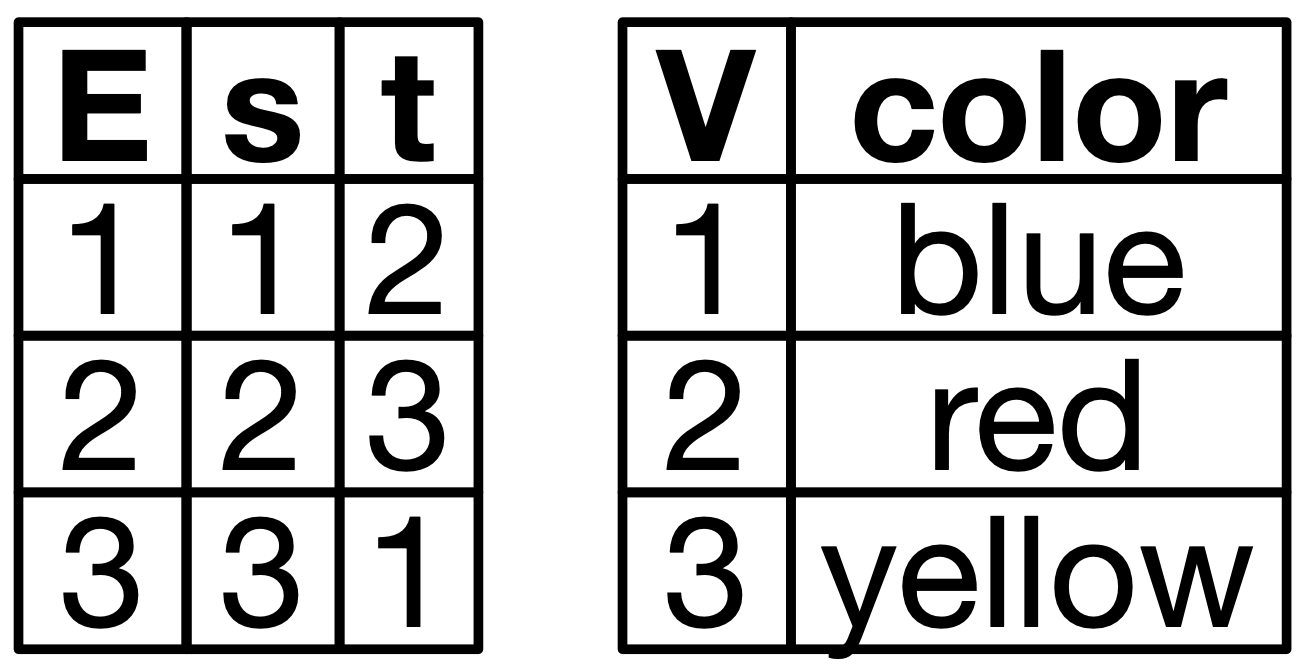
INSERT INTO VERT VALUES ('B')
INSERT INTO VERT VALUES ('R')
INSERT INTO VERT VALUES ('Y')
INSERT INTO EDGE VALUES (1,2)
INSERT INTO EDGE VALUES (2,3)
INSERT INTO EDGE VALUES (3,1)

Here is an example specific database schema. Schemas are abstractions which codify various logical constraints, such as “every edge has a source and target vertex” and “every vertex has a color”.

Below are two representations of a particular instance of this database. To the right are some SQL statements which would create such a triangle.

Abstraction: databases