Published

3/8/24

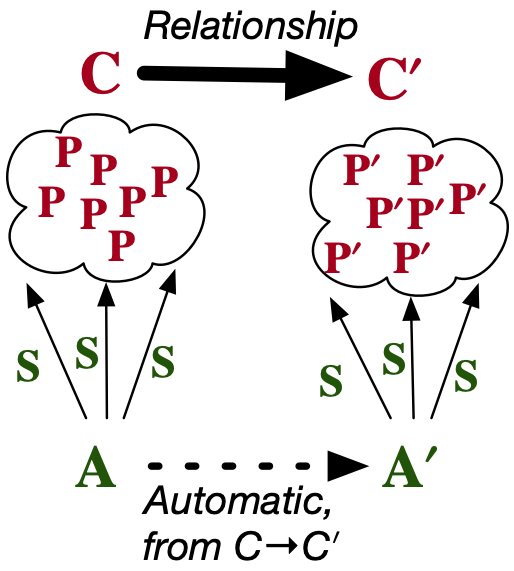
Here we simply declare the relationship between the two schemas and say how we want to interpret it (the name of action which pushes data forward along the map is called sigma and the one which moves data the opposite direction is called delta).

Replacing code with data

Theme: code vs declaring relationships between abstractions.

Problem	Julia solution	AlgebraicJulia solution
Different pieces of a model need to be glued together.	Write a script which does the gluing or modifies how pieces are constructed.	Declare how overlap relates to the building blocks. (colimits)
Different aspects of a model need to be combined / a distinction is needed.	Write a script which creates copies of one aspect for every part of the other aspect.	Declare how the different aspects interact with each other. (limits)
We want to integrate systems at different levels of granularity.	Refactor the original code to incorporate the more detailed subsystem.	Separate syntax/semantics. Declare how the part relates to the whole at syntax level. (operads)
We make a new assumption and want to migrate old knowledge into our new understanding.	Write a script to convert old data into updated data.	Declare how the new way of seeing the world (i.e. schema) is related to the old way. (data migration)

So to summarize these past toy examples, there are some very general kinds of ways that we recognize a problem has shifted and we wish to reuse our old abstractions towards the new problem. In any specific scenario, one can always write an ad hoc function or script to handle this, but once you do this time after time, these one-off solutions become unmaintainable spaghetti. This is in contrast to the eat-your-cake-and-have-it-too solution on the right, where we have general solutions which do not need to be rewritten for every new scenario that pops up. And the way these compose together is transparent.

Of course, it’s not magic, and this strategy isn’t immediately available whenever we dream up of a new domain. Structural mathematics shows us what structure to look for in a new domain that allows us to do these things, though it’s still a case-by-case process to take domain-expert’s knowledge and find this structure. In the next section I’m going to give a high level picture of how this works.

Why does it work?

Informal definition: a category is a bunch of things that are related to each other

. . .

Key intuition: category theory is concerned with universal properties.

These change something that we once thought of as a property of an object into a kind of relationship that object has towards related objects.

Goal of talk is not to communicate how category theory works at a technical level. This is why this is the only definition which will be featured in the talk. (…)

But it’s important to get an intuition for why it works to know it’s not magic. I think the philosophy of category theory, which encourages working with universal properties, is a good explanation. I’ll try to describe one example of the simplest universal property just to give you some intuition for how it works.

Example universal property: emptiness

Consider mathematical sets which are related to each other via functions.

Definition in terms of internal properties

The empty set is the unique set which has no elements in it.

But if we we look at how the empty set relates to all the other sets, we’ll eventually notice something about these relations.

. . .

Definition in terms of external relationships (universal properties)

The empty set is the unique set which has exactly one function into every other set.

So if you were to tell a high schooler what an empty set is, this is a perfectly good definition. However, it doesn’t automatically generalize to telling us what an empty matrix is, or what an empty dynamical system or graph is. (…)

Example universal property: emptiness

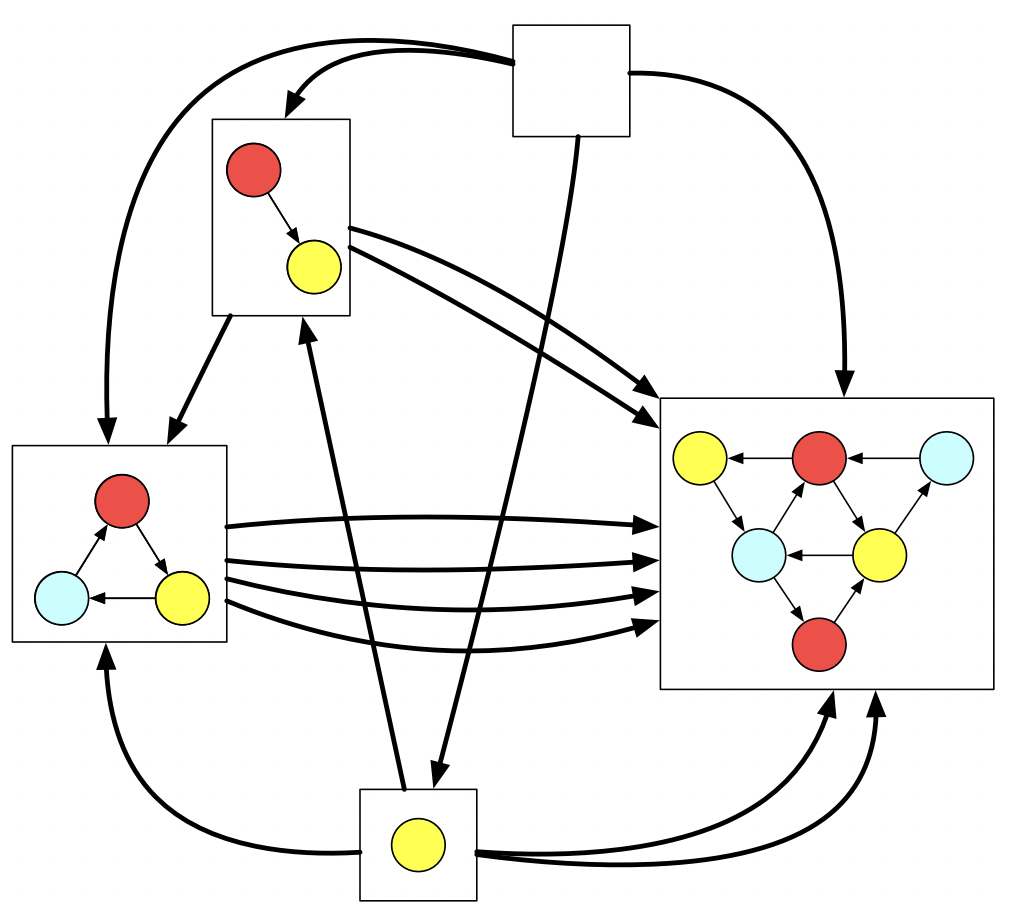
Consider colored graphs related to each other via vertex mappings which preserve color and edges.

Definition in terms of internal properties

The empty graph uniquely has no vertices nor edges in it.

But if we we look at how it relates to all the other graphs, we’ll eventually notice something characteristic.

Definition in terms of external relationships (universal properties)

The empty graph is the unique graph which has exactly one graph mapping into every other graph.

We can see that the yellow vertex lives within the triangle in one way but in the big triangle in two ways, etc. If I wanted to say why this is the empty graph, of course my first instinct would be to say “Just look at it! There are no vertices, no edges!”. But look that our same definition from earlier which says to look for the object which is related to every other object exactly once also applies here.

Universal properties and generalizable abstractions

Category theory enforces good conceptual hygeine - one isn’t allowed to depend on “implementation details” of the things which feature in its definitions.

This underlies the ability of models built in AlgebraicJulia to be extended and generalized without requiring messy code refactor.

When you structure your code around these definitions, you inherit this kind of generalizability.

Takeaways

CT is useful for the same reason interfaces are generally useful. In particular, CT provides generalized¹ notions of

multiplication / multidimensionality
adding things side-by-side
gluing things along a common boundary
looking for a pattern
find-and-replace a pattern
parallel vs sequential processes

Mad Libs style filling in of wildcards
Zero and One
A point
“Open” systems
Subsystems
Enforcing equations
Symmetry

. . .

These abstractions all fit very nicely with each other:

conceptually built out of basic ideas of limits, colimits, and morphisms.

We can use them to replace a large amount of our code with high level, conceptual data.

I hope to have shown that just a few basic concepts in category theory, in particular morphisms, limits, and colimits, are a very versatile vocabulary of good abstractions. Various combinations of these are sufficient to capture all of the diverse kinds of activities you see up here in a very generic way that can be specialized to your domain once you view it categorically.

About the Topos Institute

Vision: topos.institute
Research: topos.site
Blog: topos.site/blog

Mission: to shape technology for public benefit by advancing sciences of connection and integration.

Three pillars of our work, from theory to practice to social impact:

Collaborative modeling in science and engineering
Collective intelligence, including theories of systems and interaction
Research ethics

Physics simulations (PDEs) with Decapodes.jl
Reaction networks with AlgebraicPetri.jl
Epidemiological modeling with StockFlow.jl
Agent-based modeling with AlgebraicRewriting.jl
Interactive GUIs with Semagrams

Decapodes.jl: multiphysics modeling

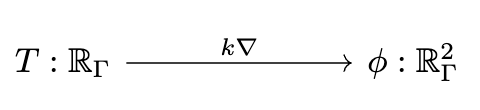
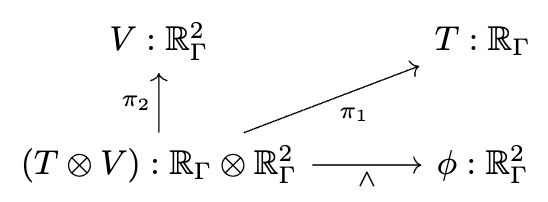
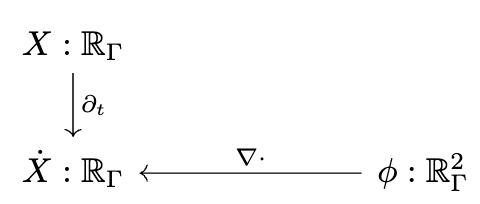
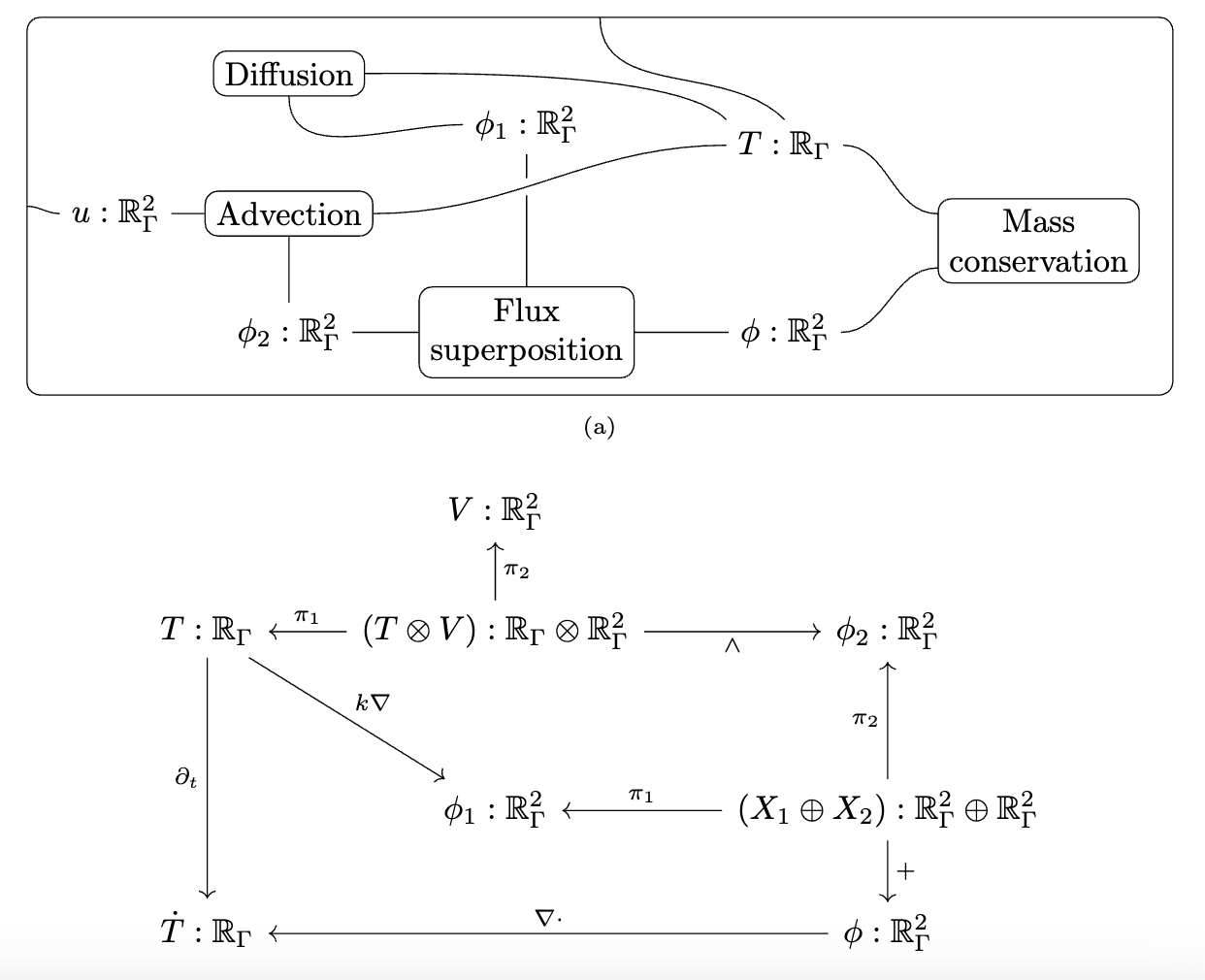
"""Define the multiphysics"""
Diffusion = @decapode DiffusionQuantities begin
  C::Form0{X}
  ϕ::Form1{X}
  ϕ == k(d₀{X}(C))   # Fick's first law
end
Advection = @decapode DiffusionQuantities begin
  C::Form0{X}
  (V, ϕ)::Form1{X}
  ϕ == ∧₀₁{X}(C,V)
end
Superposition = @decapode DiffusionQuantities begin
  (C, Ċ)::Form0{X}
  (ϕ, ϕ₁, ϕ₂)::Form1{X}
  ϕ == ϕ₁ + ϕ₂
  Ċ == ⋆₀⁻¹{X}(dual_d₁{X}(⋆₁{X}(ϕ)))
  ∂ₜ{Form0{X}}(C) == Ċ
end
compose_diff_adv = @relation (C, V) begin
  diffusion(C, ϕ₁)
  advection(C, ϕ₂, V)
  superposition(ϕ₁, ϕ₂, ϕ, C)
end

"""Geometry"""
mesh = loadmesh(Torus_30x10())

"""Assign semantics to operators"""
funcs = sym2func(mesh)
funcs[:k] = Dict(:operator => 0.05 * I(ne(mesh)), 
  :type => MatrixFunc())
funcs[:⋆₁] = Dict(:operator => ⋆(Val{1}, mesh, 
  hodge=DiagonalHodge()), :type => MatrixFunc());
funcs[:∧₀₁] = Dict(:operator => (r, c,v)->r .= 
  ∧(Tuple{0,1}, mesh, c, v), :type => InPlaceFunc())

Extending what I’ve said so far to the design of simulators amounts to the following:

simulations should be compiled to code rather than written in code
This is because we can do high level conceptual programming (e.g. limits and colimits) when we are working with data, whereas representing our simulation via code will forever condemn us to having every conceptual update require a painstaking manual code update that could be very challenging.

When we work at the low level of code, introducing a simple mathematical idea (for example adding a gravitation force) forces us to remind ourself of all the implementation details - there could be a cascade of changes required.

I can only briefly gesture at the work done by some of my colleagues in a compositional language for multiphysics. The idea is that there is a graphical language for specifying equations which rigorously corresponds to things like Fick’s law of diffusion and conservation of mass. This is just like how our Petri Nets were a nice graphical language which could rigorously be interpreted as Chemical Reaction Networks and how spans of models can be rigorously interpreted as models glued along an overlap.

There is some interesting math behind how this works which I won’t be able to get into, involving something called the “discrete exterior calculus”, but from a user perspective you can see us declaring each of these small diagrams and then composing them together along shared variables into a multi-physics. We then need to give a computational semantics by associating linear operators with some of the primitive building blocks, such as “multiplication by k” being 0.05 times the identity matrix.

We decoupled the high level physics from the geometry and the implementation.

Decapodes.jl: simulation

Resources

Papers and talks: algebraicjulia.org
Blog posts: algebraicjulia.org/blog and topos.site/blog
Code: github.com/AlgebraicJulia

If you want to follow up on any the ideas in this talk, we have lots of papers, a couple of which I point out here to be potentially of interest to scientists. We also write blog posts intended to be more accessible and conversational, and I highlight a few here. Our code is always open source and we’re delighted to see it getting used. Lastly the talk itself is available online on my website, in case you want to click on links or see things in more detail (You can also see my extensive speaker notes there).

Hidden slide: this slide intentionally left blank

You’re not supposed to be here.

Hidden slide: Why Category Theory?

Focuses on relationships between things without talking about the things themselves.

Invented in the 1940’s to connect different branches of math.

. . .

A category consists of objects and morphisms (arrows).

We don’t need to know anything about the objects.
Compose \(A \rightarrow B\) and \(B \rightarrow C\) to get \(A \rightarrow C\).
Like a graph, but we care about paths, not edges.

. . .

CT studies certain shapes of combinations of arrows.

These can be local shapes, e.g. a span: \(\huge \cdot \leftarrow \cdot \rightarrow \cdot\)
These can be global, e.g. an initial object: \(\huge \boxed{\cdot \rightarrow \cdot\rightarrow \cdot \rightarrow \dots}\)

Let me introduce just enough about CT to explain how it could, in principle, be useful. [read slide]

Hidden slide: Applied Category Theory?

Compare to interfaces in computer science:

declare that some collection of things are related in a particular way without saying what they are.

interface Queue{A}

size(q:Queue) -> Int 
empty(q:Queue) -> Bool 
put(q:Queue, a:A) -> ()
get(q:Queue) -> A

. . .

In some sense a category is just a particular interface.

interface Category{Ob,Arr}

dom(a:Arr) -> Ob 
codom(a:Arr) -> Ob 
compose(a:Arr, b::Arr) -> Arr 
id(o:Ob) -> Arr

Category of sets and functions
Category of sets and subsets
Category of \(\mathbb{Z}\) and \(\leq\)
Category of categories and functors

Category of chemical reaction networks
Category of chemical structures
Category of datasets
Category of datatypes and programs

. . .

CT is also the study of interfaces in general. It knows which are good ones.

Let me try to connect this to a computer science concept you may be familiar with. In computer science you might declare an interface without caring how its specifically implemented. Programmers quickly learn that this kind of abstraction is really useful because your code can be much less brittle when it doesn’t make assumptions about the intrinsic nature of the things it interacts with: for example you start out with a linked-list implementation of a queue, but later you learn you need to switch to a vector implementation for performance reasons. None of your code had to break.

. . .

If you want to know how something abstract like category theory can be useful, first think of it as an interface for which mathematicians have been writing code for over the last century. All you need to do is show how chemical reaction networks implement the interface of a category and suddenly you have access to a rich library of questions to ask about your domain (e.g. what does a span or initial object correspond to?) and furthermore there is a formalism to relate different categories to each other, so you can make connections between different domains explicit.

. . .

The last thing I’ll say on this topic is that a category codifies caring about how things relate to each other without looking at the things themselves. So it is also an opinionated source of what are good interfaces.

Footnotes

Defined by universal properties.↩︎