With AlgebraicJulia, rather than just having the flowchart be something that inspires us from the whiteboard to write some code, we reason about it as a piece of data. The code we would’ve written is constructed automatically by saying what goes in each box and having a mathematical understanding of what is in general required to go from saying what is in each box to saying what the outer box does.
Changing from one abstraction to another
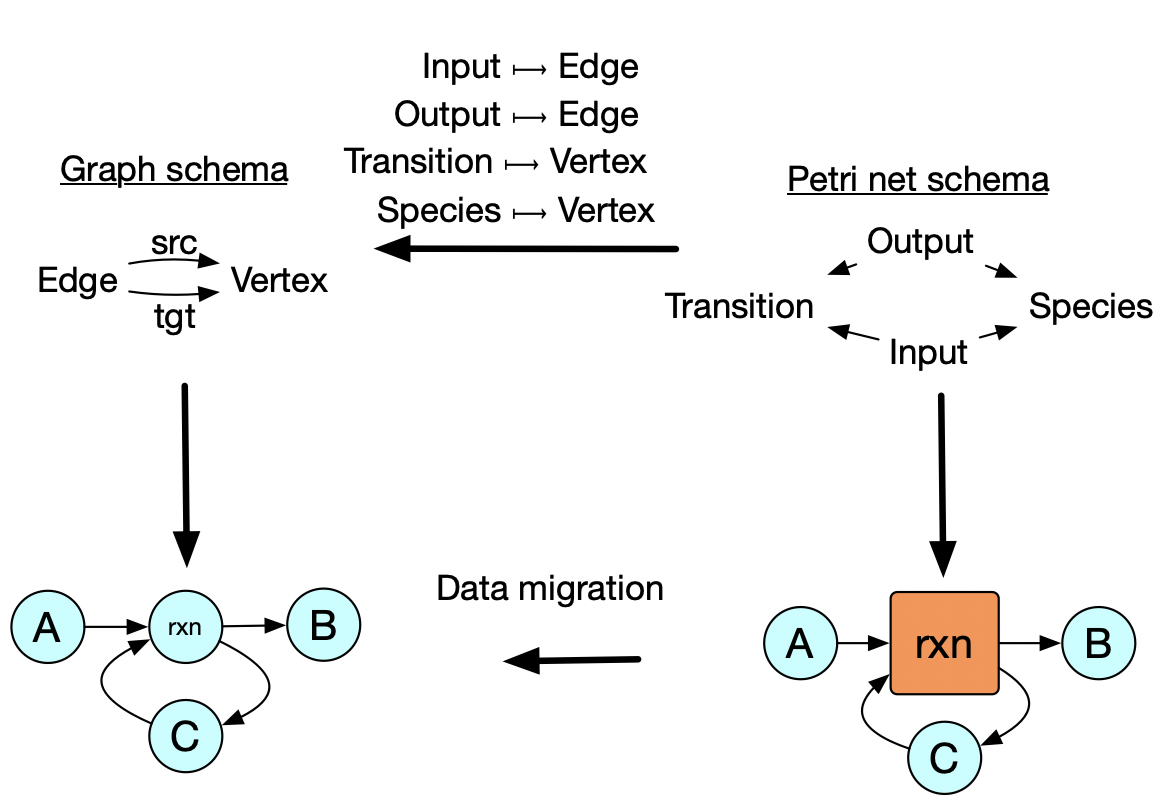
In addition to the previous examples which show re-use of abstractions within each of the three data types, this example shows how we can preserve an abstraction even when we change the data type: one might write a chemical reaction simulator that accepts Petri nets, but for other parts of one’s analysis one might not be working with general Petri nets. There are many algorithms and concepts that make sense for ordinary directed graphs that don’t make sense for Petri nets, so one ought work for as long as possible in the restricted setting with the knowledge that, at the end, one can identify graphs with a special kind of Petri net (i.e. those which have transitions with exactly one input and one output). What may be surprising is that this transformation process is completely automated, just given a simple relationship between the two database schemas at the top. Structural mathematics tells us how to specify the relationships between specifications such that implementations can be migrated from one to the other in a meaning-preserving way.
Changing from one abstraction to another
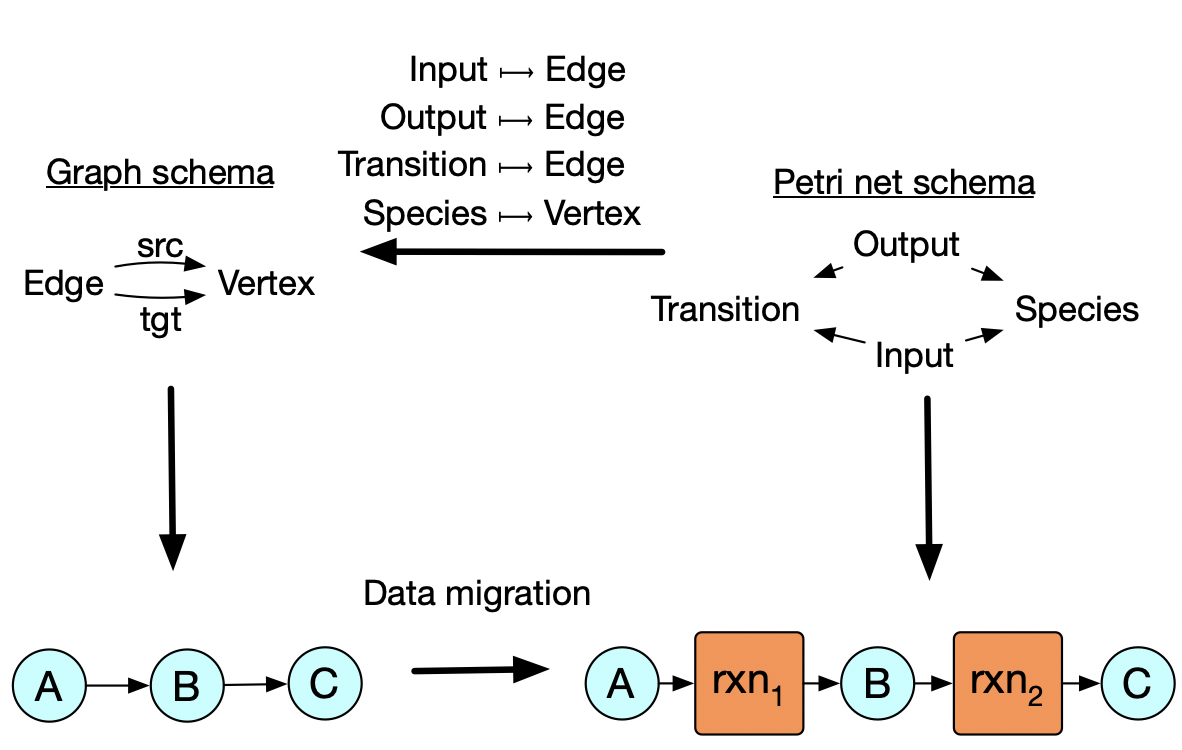
This high level data to relate the two schemas can be also used to move data in the other direction. So maybe what we need at the end of the day is a petri net, but we want to do our fancy graph algorithms with certain graphs and then convert them to Petri nets at the end.