Inferentialism and applied category theory
Kris Brown - August 17, 2024
Logic, Methodology of Science & its Applications

8/17/24
Two related problems: scientific communication
$$
$$
What framework for cooperation doesn’t trap us in our present misconceptions?
- Need some sort of fixed structure / common protocol in order to communicate
- However: fixed structures may bake in unknown assumptions we’ll want to change
Alice and Bob study a very basic form of chemistry, and find it productive to communicate their theories and discoveries to each other via messages like “\(A\rightarrow B\), \(B\rightarrow C\), \(C\rightarrow A\)”. If everyone were to buy into this protocol, one could write software which checks things like “Is anyone else studying reaction networks with \(A\) and \(C\)?” or “Is there a pathway that gets me from \(A\) to \(D\)?”
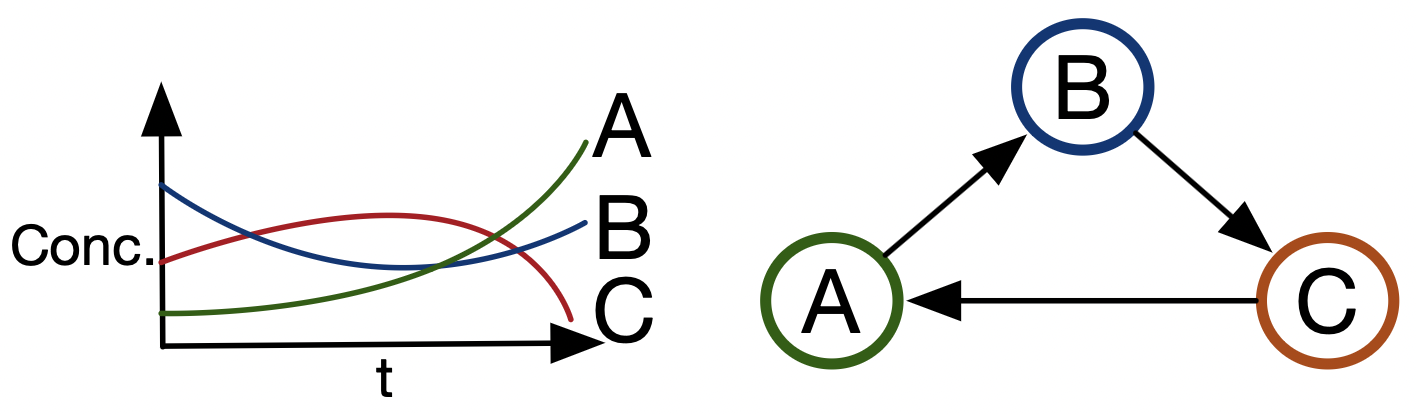
Two related problems: scientific communication
What framework for cooperation doesn’t trap us in our present misconceptions?
Chris also studies chemistry. He’d like to communicate with her too via messages; however, what she calls ‘A’ he calls ‘B’, and he thinks what she calls ‘B’ and ‘C’ are actually both the same thing, ‘D’. They end up not collaborating.
Alice and Bob later discover that they find it much more productive to analyze some phenomena as “multi-reactions”, where one can have multiple inputs and outputs. They could modify their code to add a new data structure: “A + B \(\Rightarrow\) C + D, A \(\rightarrow\) B”, but this will be a lot of work (so for the time being, they continue to use singular reactions).
Alternatively they could consider their old notion of ‘reaction’ to be inadequate: that they thought were reactions are ‘multi-reactions’. But the same practical problem remains.
Can we find a synthesis of structure and flexibility?
Two related problems: semantics
How do we think about semantics in a way that’s amenable to redescription?
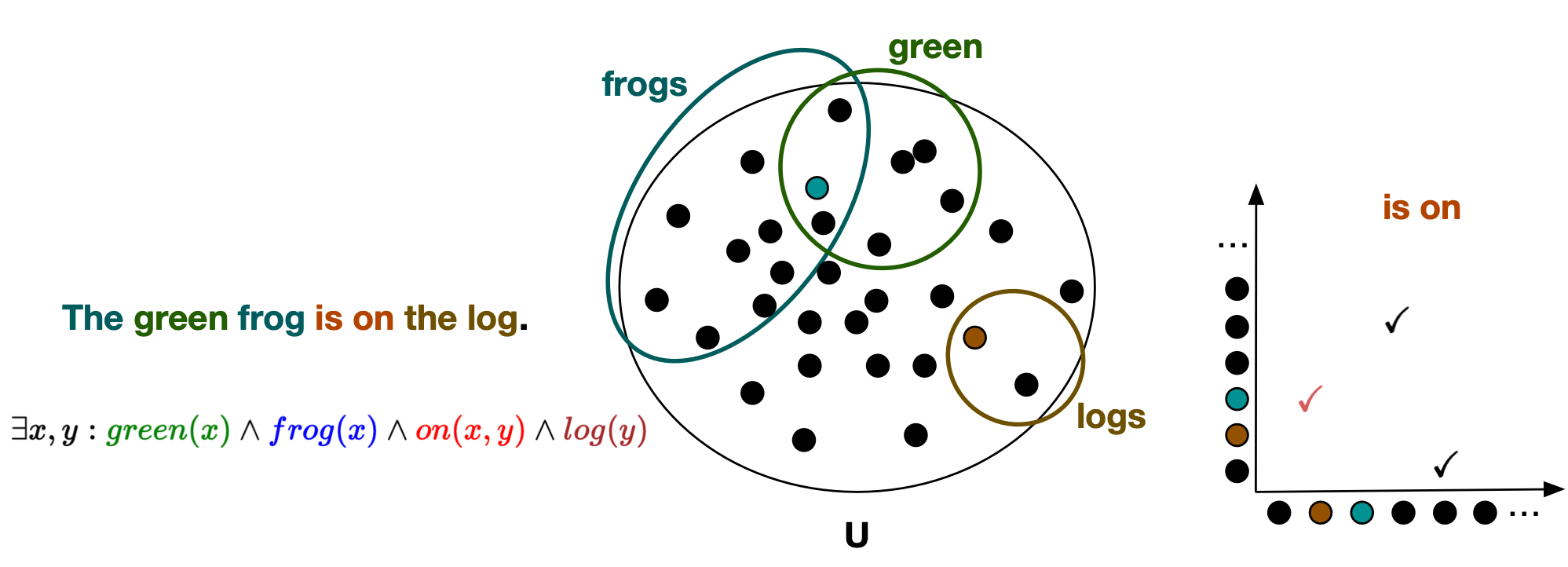
Compositionality: understanding each component’s meaning allows one to determine the overall statement’s meaning.
Two related problems: semantics
How do we think about semantics in a way that’s amenable to redescription?
- In order to qualify as a semantics, we need compositionality. (E.g. truth conditions)
- Semantics traditionally casts meanings in stone (fixed meanings determine proper use), whereas redecription is a process in the opposite direction.
If I can’t work, then I don’t deserve food … unless food is a human right.
If it’s a cat, then it’s a mammal…unless future scientists discover cats are actually aliens.
The electron is at position \(p\) with velocity \(v\)… but then we learn Heisenberg uncertainty.
The triangle has more than 180 degrees… but the triangle is not a planar triangle.
Can we obtain compositionality without meaning constituted by fixed truth conditions?
Outline
Two approaches to a common kind of problem
- Work in categorical logic at the Topos Institute:
- Broaden notions of logic and semantics
- Make shifting foundations ergonomic
- Pluralist computational science
Work in infentialist semantics: logical expressivism
- Rethink the relationship between logic and reasoning
- Open reason relations
Background: Category Theory
Focuses on relationships between things without talking about the things themselves.
CT studies certain shapes of combinations of arrows.
These can be local shapes, e.g. a span
These can be global, e.g. an initial object:

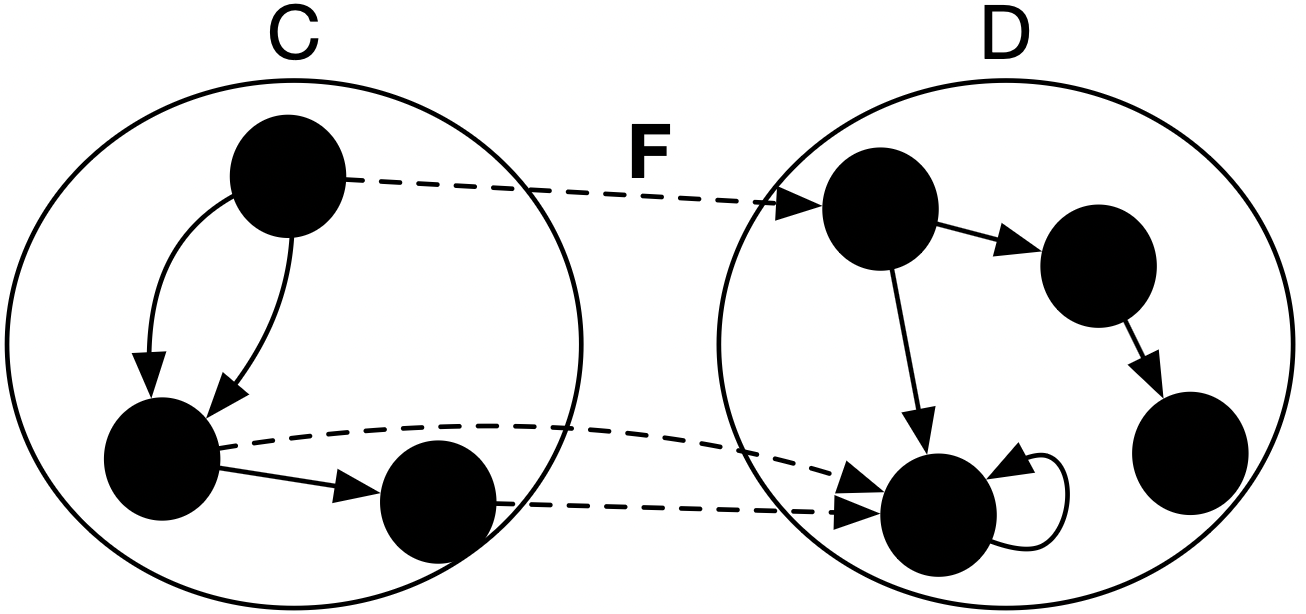
- Functors \(F: \mathsf{C}\rightarrow \mathsf{D}\) are assignments objects and arrows of \(\mathsf{C}\) to those in \(\mathsf{D}\) that respect the local structure of \(\mathsf{C}\).
Power of CT to abstract comes from the fact its definitions can be applied in any category.
Its definitions don’t require that its subject matter be anything in particular, rather they make pre-existing structure explicit.
ACT and scientific pluralism: functorial semantics
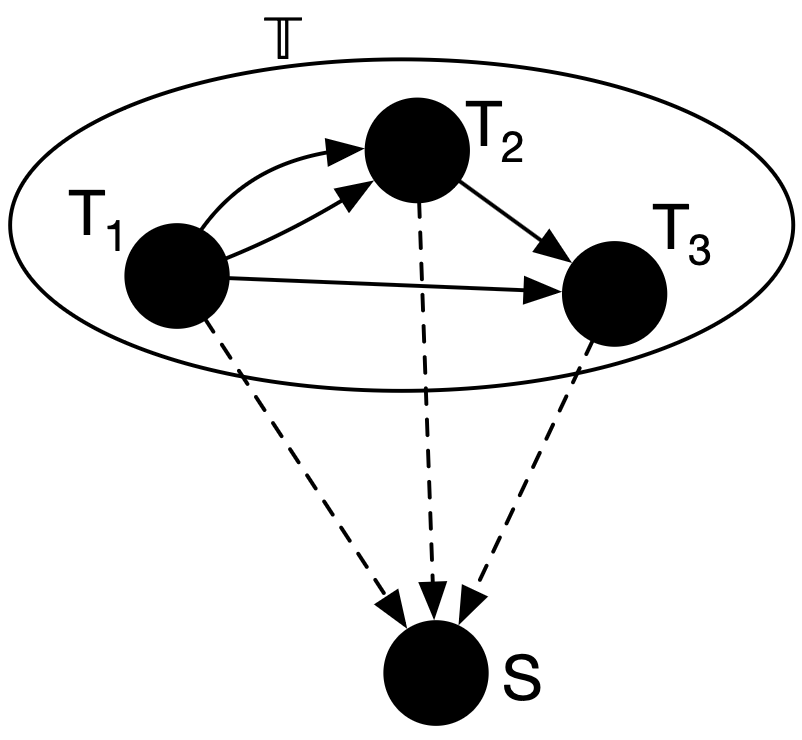
In this diagram, theories \(T_1,T_2,T_3\) are categories. We specify the semantics of a theory by giving a functor from the theory to a semantics category \(S\). Let \(S = \mathbf{Set}\) for now.
- No need to be confined to a single theory (nor reducible to a single theory)
- No need to be confined to a fixed semantics1
- A meta-theory \(\mathbb{T}\) (or doctrine) defines a space of theories
- Higher category theory allows us to iterate this procedure as needed.
Example scientific model: Petri nets
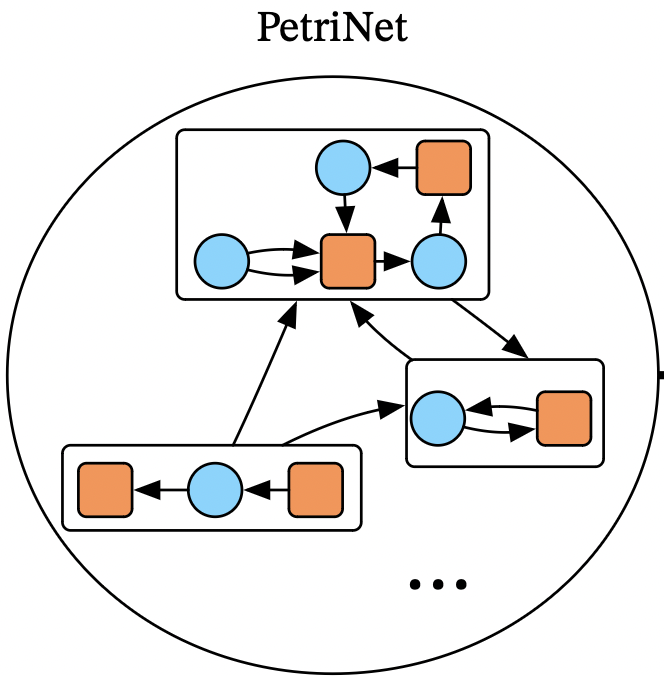
Petri nets consist of species and transitions, connected by input and output arcs.
We can of these as a syntax for chemical reaction networks:
- 🔵 The species are chemical species
- 🟧 The transitions are chemical reactions
- The inputs/outputs tell you how many of each molecule is a reactant/product
The category of all Petri nets is the category of models of a particular theory.
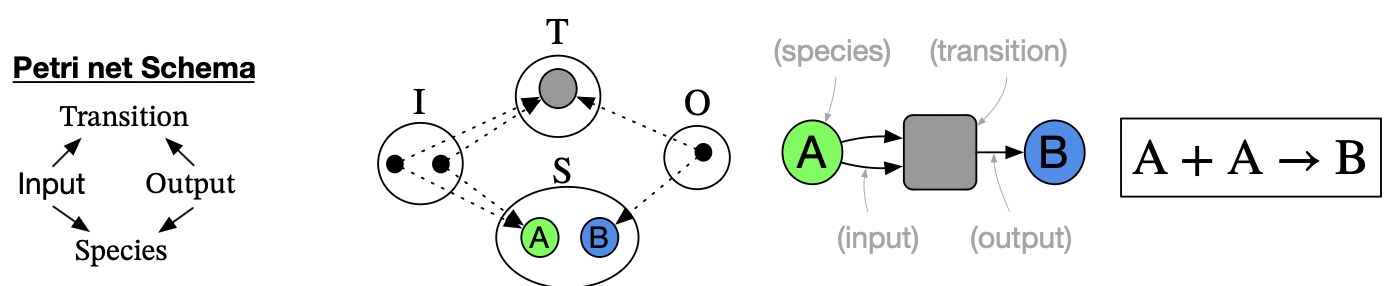
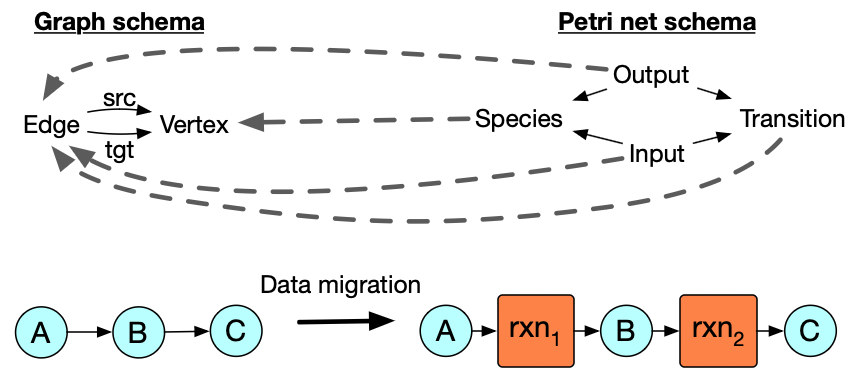
Theories for graphs and Petri nets
Let’s return to our first example. We want to redescribe our earlier notion of reaction as a one-in-one-out relationship to a many-in-many-out relationship between species.
Reaction networks in the former paradigm are graphs, which have two sets and two functions.

Petri nets describe the new paradigm of reaction networks. Petri nets consist in four sets and four functions.
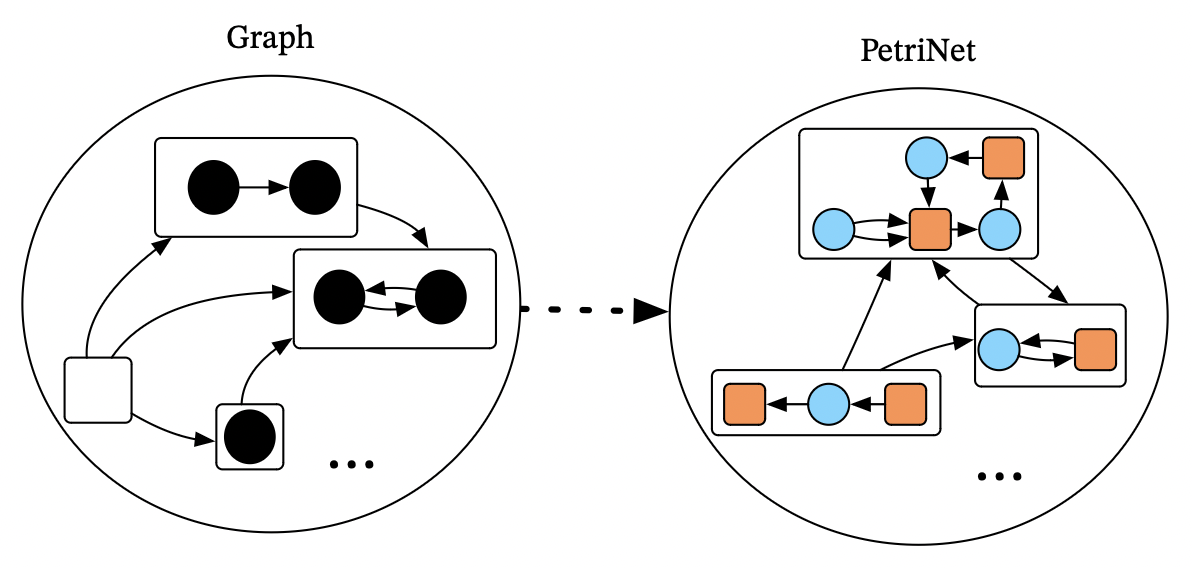
Example: data migration of graphs to Petri nets
What we want is a way of systematically turning our graphs into Petri nets
- I.e. a functor from category of graphs to category of Petri nets
- However, involves a massive amount of data.
Example: data migration of graphs to Petri nets
What we want is a way of systematically turning our graphs into Petri nets
- I.e. a functor from category of graphs to category of Petri nets
- However, involves a massive amount of data.
Conceptually-legible way to packaging this: merely need a functor between the two schemas.
Functorial data migration redescribes graph-vocabulary as Petri net vocabulary.
Example: open Petri nets
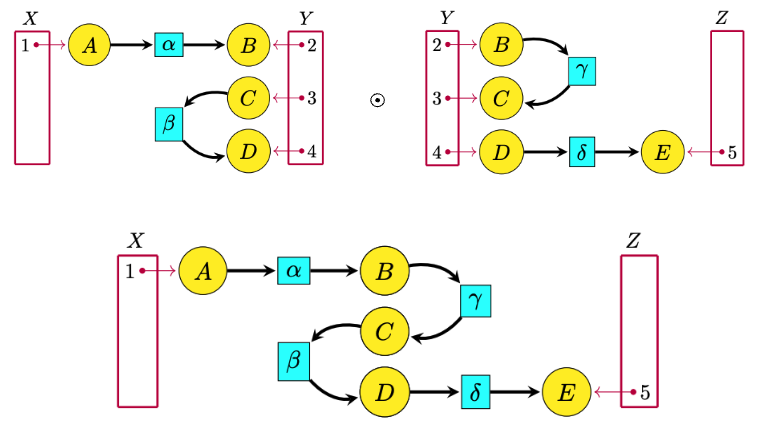
The category of Petri nets can be given 2-dimensions of composition1
ACT can systemically construct ‘open’ versions of models and assign functorial semantics.
Closed systems are a special case of a system with an empty boundary.
One integrates more (previously unknown) information by composing one’s model.
ACT: key points
- CT works with external structure rather than internal structure
- Categories use universal properties to make a category’s pre-existing structure explicit
- Logic is interpreted within any category if it has enough structure for it (pluralism)
- Emphasis on open systems rather than closed systems
- One can reason within a theory while retaining flexibility
- Syntax and semantics are both categories, rather than two different kinds of things
- Mathematically-justified notions of redescription, e.g. functorial data migration

Inferentialism

Inferentialist theories of meaning prioritize inferential role over reference in the order of explanation.
An ongoing practice of giving and asking for reasons is the starting point, rather than than the end point.
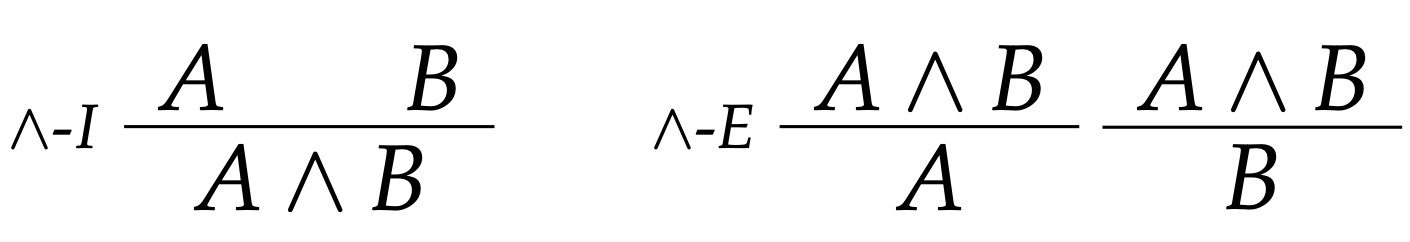
What and means is captured entirely by its circumstances of application and consequences of application. No account of reference needed.
Can we do this with our ordinary concepts, too?
Reason relations, implication frames
Suppose we have a base lexicon of claimables \(L_B = \{a,b,c,d,...\}\).
Reason relations among these claimables look like “\(a,b \mid\hspace{-0.1em}\sim c,d\)” (implication) and “\(a,b \mid\hspace{-0.1em}\sim\ \)” (incompatibility). The space of possible implications/incompatibilities is \(S_B = \mathscr{P}(L_B)^2\). An implication frame (or ‘vocabulary’), \((L_B, \mathbb{I}_B)\), endorses a subset \(\mathbb{I}\subseteq S_B\) of these reason relations, which Restall suggests we read as a claim of incoherence:
\[(\Gamma,\Delta) \in \mathbb{I} \text{ means rejecting all of } \Delta \text{ and accepting all of } \Gamma \text{ is incoherent}\]
The notion of a vocabulary here is very broad:
- \(a =\) “It is pious” and \(b =\) “It is loved by the gods” \(a\mid\hspace{-0.1em}\sim_{TL} b\) (some kind of theological vocabulary)
- \(x =\) “Pittsburgh is to the west of NY” and \(y =\) “NY is to the east of Pittsburgh”, then \(x \mid\hspace{-0.1em}\sim_{OL} y\) (ordinary language / material inference)
- \(a =\) “\(\forall m,n, eastOf(m,n) \iff westOf(n,m)\)”, \(b =\) “\(westof(P,NY)\)” and \(c =\) “\(eastof(NY,P)\)”, then \(a,b\mid\hspace{-0.1em}\sim_{FOL} c\) (first-order logic)
Logical expressivism
Claim: logic makes reason relations explicit: \(\Gamma \mid\hspace{-0.1em}\sim a \rightarrow b\) says that \(\Gamma, a \mid\hspace{-0.1em}\sim b\).
We can extend any base lexicon to include logically-complex claimables, e.g. \(a \land b\): what then of the reason relations between these new claimables, or implications that mix base claimables and logical ones?
A framework for talking about reason relations shouldn’t impose restrictions on what is a ‘good’ implication frame: chemists, theological scholars, relevance or paraconsistent logicians, etc. all have their own expertise. Yet many of these, while still be rational, fail to obey monotonicity and transitivity. Classical logic is not harmonious in these cases.
Example of non-harmonious rules of inference:
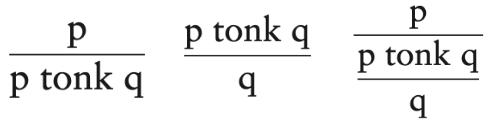
Logic should be LX: elaborated from a base vocabulary and expressive of it. Being universally LX means this is the case for any base vocabulary.
Logicism vs logical expressivism
| Logicism | Logical expressivism | |
|---|---|---|
| Logic ought study relations between | sentences with only logical vocabulary | sentences with logical vocabulary and sentences in a base vocabulary |
| Reason relations and logical vocabulary | Reason relations should be reducible to logical vocabulary | Reason relations should be expressible by logical vocabulary |
| Genuine nonlogical content, material inferences | Not possible (it’s just incompletely-specified) | Possible (fever, cruel, birds can fly, torture is wrong) |
| Search for generality | Exhibit all (doxastic) reasons as covertly logical reasons | Find a logic which is universally LX |
NonMonotonic, MultiSuccedent logic
NMMS are Gentzen-style sequent calculi which conservatively extend implication frames.
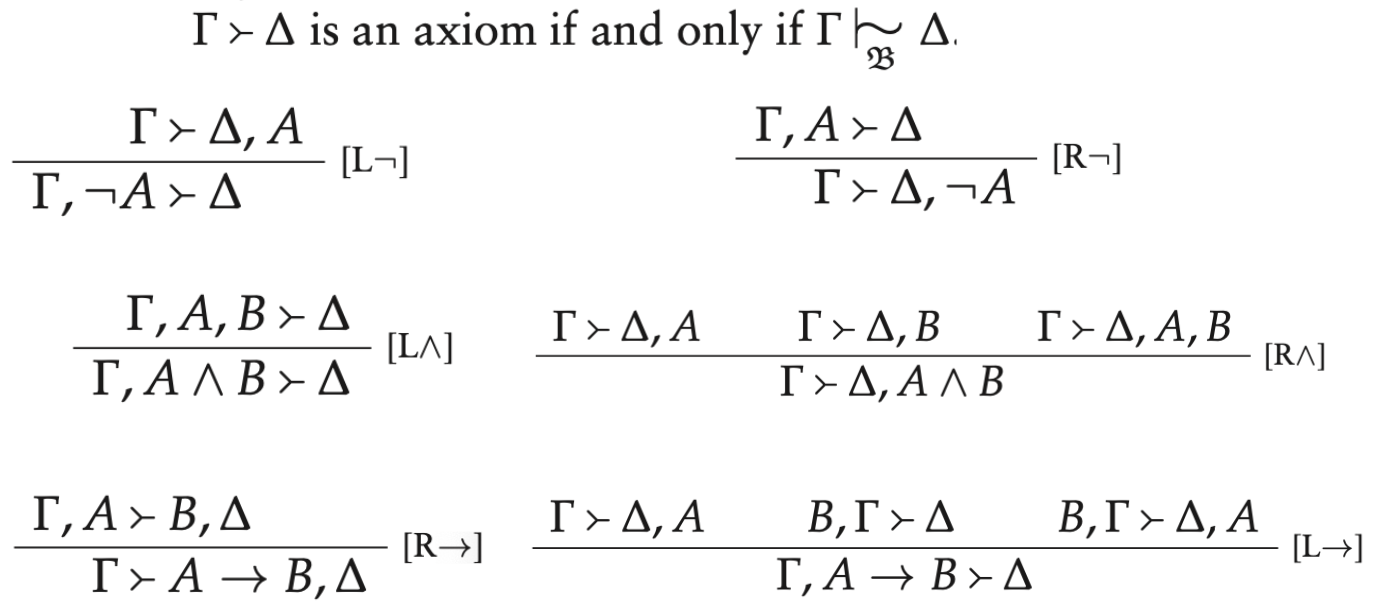
Syntax and semantics on the same playing field
Rather than arguing for truth-taking (pragmatic) to be conceptually prior to truth-making (semantic), they are shown to have a remarkable common structure:
Truth-maker theory, as developed by Kit Fine:
generalizes possible-worlds semantics by being hyperintentional: can distinguish meanings that are still true in all possible worlds, such as \(1+1=2\) and \(isPrime(3)\).
It does this via notions of worldly states, combining states, and impossible states.
One can understand the meaning of \(\Gamma \vdash \Delta\) as “there isn’t any possible state that makes every sentence in \(\Gamma\) true and every sentence in \(\Delta\) false”
Every consequence relation that can be codified in an NM-MS system over a material semantic frame can also be codified in truth-maker theory, and vice versa.
Open reason relations
Traditionally, logical consequence is closed:
\[Cn(\Gamma) = Cn(Cn(\Gamma))\ \ \ \ \ \ \ \Gamma\subseteq\Delta \implies Cn(\Gamma)\subseteq Cn(\Delta)\]
This notion forces, from the outset, for nothing to change if we had \(\Gamma \mid\hspace{-0.1em}\sim \alpha\) and decided to add \(\alpha\) back in as a premise: if \(\Gamma, \alpha \mid\hspace{-0.1em}\sim \beta\) then it was already a conclusion all along \(\Gamma \mid\hspace{-0.1em}\sim \beta\)
But this is essential to rationality: we derive consequences which, if we accept them as our new premises, allow us to derive new things, which may invalidate earlier premises or rectify earlier contradictions. Explosion is implausible for non-logical conceptual contents.
Rational hysteresis in science: we use theories to extract consequences from data, though this data can make us change our theories (yield consequences incompatible with our premises) and then the new theory extracts even newer consequences.
A fixed implication frame can capture the steps of this evolutionary process as rational steps.
\[\Gamma, a, \mid\hspace{-0.1em}\sim b,c\ \ \ \ \ \Gamma,a,b,c \mid\hspace{-0.1em}\sim\ \ \ \ \ \ \Gamma,b \mid\hspace{-0.1em}\sim c \ \ \ \ \ \ \Gamma,c \mid\hspace{-0.1em}\sim b\]
Strong and weak compositionality
Traditional semantics obeys a strong compositionality property
- “Knowing every mentioned small sentence in \(\varphi\) will enable knowing complex sentence \(\varphi\).”
Inferentialism satisfies a weaker (but nontrivial) compositionality property
- “Knowing all small sentences lets you know all complex sentences.”
Definitions in implication space are recursive but not strongly compositional.
\[\mathsf{R}(\Gamma\mid\hspace{-0.1em}\sim\Delta) := \{(X,Y) \in S\ |\ \Gamma,X\mid\hspace{-0.1em}\sim Y,\Delta \in \mathbb{I}\}\]
\[ ⟦(\neg a)^+⟧ := ⟦a^-⟧ \ \ \ \ ⟦(\neg a)^-⟧ := ⟦a^+⟧\]
\[ ⟦(a \rightarrow b)^-⟧ := ⟦a^+⟧\sqcup ⟦b^-⟧\]
\[ ⟦(a \rightarrow b)^+⟧ := ⟦a^-⟧\sqcap⟦b^+⟧\sqcap (⟦a^-⟧\sqcup ⟦b^+⟧)\]
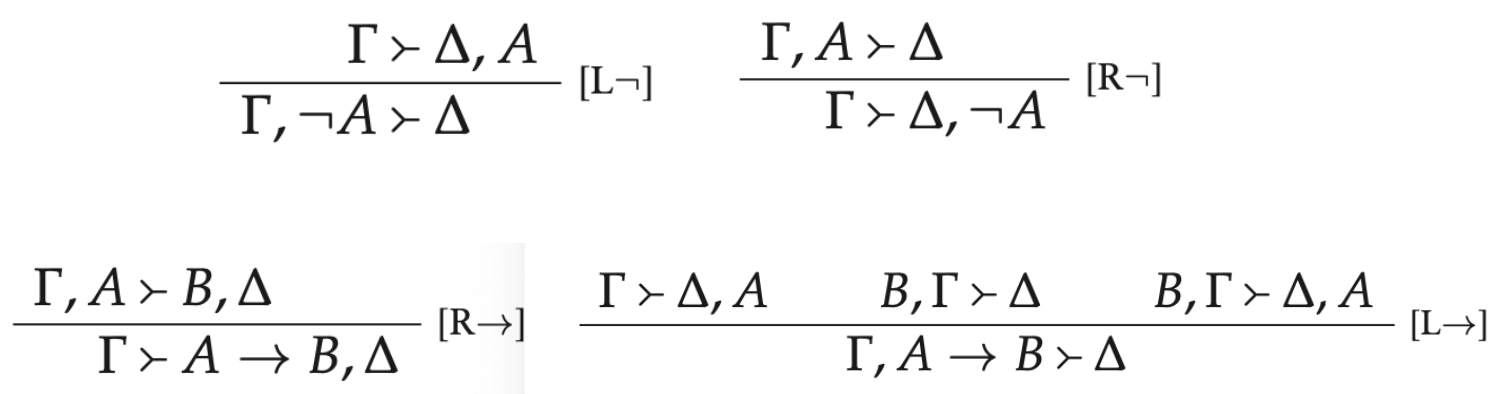
Conclusions
Remarkable similarities between ACT and logical expressivism
- Focus on making pre-existing structure explicit
- Content in terms of external structure rather than internal structure
- Logical structure is special but not guaranteed. Pluralism about the ‘right’ logic.
- Traditional thinking about logic can be good/useful, but not as a foundation
- Emphasis on open systems / reason relations
- Theoretically ground norms that are binding without fixed foundations
- Syntax and semantics on a par, rather than a gulf between fundamentally different things.
- A capacity to make sense of redescription
Thanks for listening!
And special thanks to:
Kevin Carlson, David Spivak, Owen Lynch (Topos Institute)
Ryan Simonelli (U Chicago), Ulf Hlobil (Concordia), Bob Brandom (U Pittsburgh)
Speculative parallels: the two-language problem
| Universality: impractical and restrictive norms | Contingency: norms profilerate, fail to legitimately bind us | |
|---|---|---|
| Protocols | Semantic web: universal ontology but illegible, inflexible, clunky | Domain-specific languages: fragmented, no interoperability, only local legibility |
| Semantics | Representionalism: mind as mirror of nature | Poststructuralism/regularism: language games all the way down, no reason for cooperation |
Solution is to contextualize the locally-authorative norms, allow them to talk to each other.
Can only be done from a vantage point that does not presuppose the content of what it’s talking about.
