using Catlab
g = path_graph(Graph, 3)| E | src | tgt |
|---|---|---|
| 1 | 1 | 2 |
| 2 | 2 | 3 |
Kris Brown, David Spivak - ACT 2023

(press s for speaker notes)
8/1/23
$$
$$

function ca_step!(model)
new_status = fill(false, nagents(model))
for (agid, ag) in model.agents
nlive = nlive_neighbors(ag, model)
if ag.status == true && (nlive ≤ model.rules[4] && nlive ≥ model.rules[1])
new_status[agid] = true
elseif ag.status == false && (nlive ≥ model.rules[3] && nlive ≤ model.rules[4])
new_status[agid] = true
end
end
for k in keys(model.agents)
model.agents[k].status = new_status[k]
end
endmutable struct Agent <: AbstractAgent
id::Int; pos::NTuple{2,Float64}
vel::NTuple{2,Float64}; mass::Float64
endfunction elastic_collision!(a, b, f = nothing)
v1, v2, x1, x2 = a.vel, b.vel, a.pos, b.pos
length(v1) != 2 && error("This function works only for two dimensions.")
r1 = x1 .- x2; r2 = x2 .- x1
m1, m2 = f == nothing ? (1.0, 1.0) : (getfield(a, f), getfield(b, f))
!(dot(r2, v1) > 0 && dot(r2, v1) > 0) && return false
f1,f2 = (2m2/(m1+m2)), (2m1/(m1+m2))
ken = norm(v1)^2 + norm(v2)^2
dx = a.pos .- b.pos
dv = a.vel .- b.vel
n = norm(dx)^2
n == 0 && return false # do nothing if they are at the same position
a.vel = v1 .- f1 .* ( dot(v1 .- v2, r1) / n ) .* (r1)
b.vel = v2 .- f2 .* ( dot(v2 .- v1, r2) / n ) .* (r2)
return true
endcreate-sheep initial-number-sheep ; create the sheep, then init vars
[
set shape "sheep"
set color white
set size 1.5 ; easier to see
set label-color blue - 2
set energy random (2 * sheep-gain-from-food)
setxy random-xcor random-ycor
]to eat-sheep ; wolf procedure
let prey one-of sheep-here ; grab a random sheep
if prey != nobody [ ; did we get one? if so,
ask prey [ die ] ; kill it, and...
set energy energy + wolf-gain-from-food ; get energy from eating
]
end
to death ; turtle procedure (i.e. both wolf and sheep procedure)
; when energy dips below zero, die
if energy < 0 [ die ]
end; stop the model if there are no wolves and no sheep
; stop the model if there are no wolves and the number of sheep gets very large
if not any? wolves and count sheep > max-sheep [ user-message "The sheep have inherited the earth" stop ]
ask sheep [
move
; in this version, sheep eat grass, grass grows, and it costs sheep energy to move
if model-version = "sheep-wolves-grass" [
set energy energy - 1 ; deduct energy for sheep only if running sheep-wolves-grass model version
eat-grass ; sheep eat grass only if running the sheep-wolves-grass model version
death ; sheep die from starvation only if running the sheep-wolves-grass model version
]
reproduce-sheep ; sheep reproduce at a random rate governed by a slider
]
ask wolves [
move
set energy energy - 1 ; wolves lose energy as they move
eat-sheep ; wolves eat a sheep on their patch
death ; wolves die if they run out of energy
reproduce-wolves ; wolves reproduce at a random rate governed by a slider
]General-purpose code not a great syntax for scientific modeling
Some desired properties for a model representation:
Transparent / verifiable / visualizable
Serializable + Implementation-agnostic
Flexible, e.g.
But these properties do tend to follow from giving a nice syntax category (e.g. presheaves, Poly) a computational semantics.
Rewrite rules (e.g. DPO, SPO) are a good syntax for small / local changes

How can we design a model with rewrite rules as primitive building blocks?
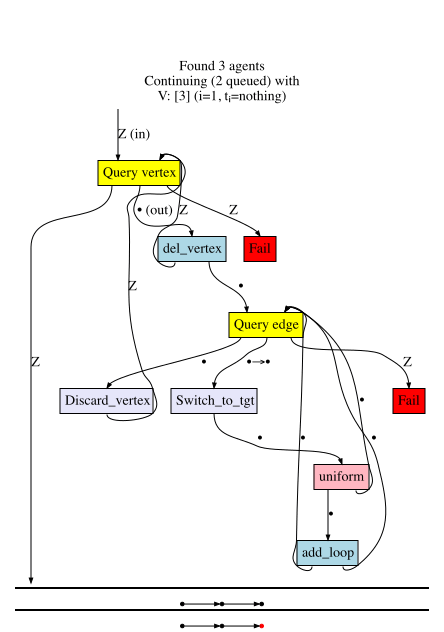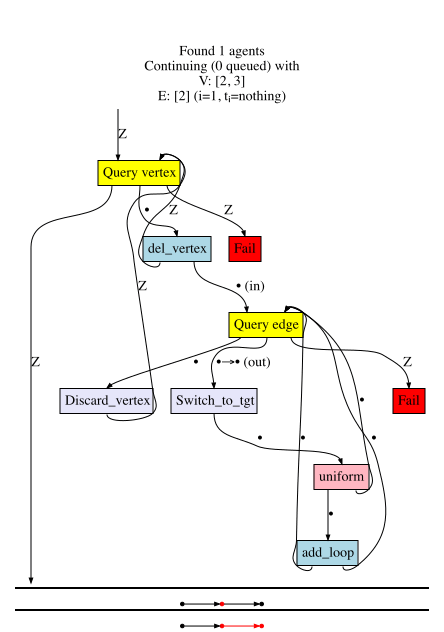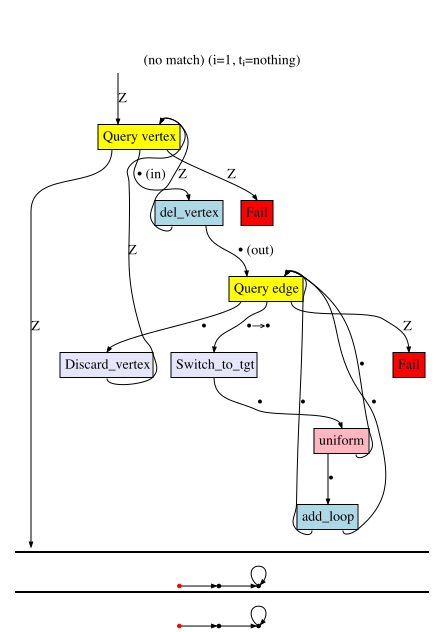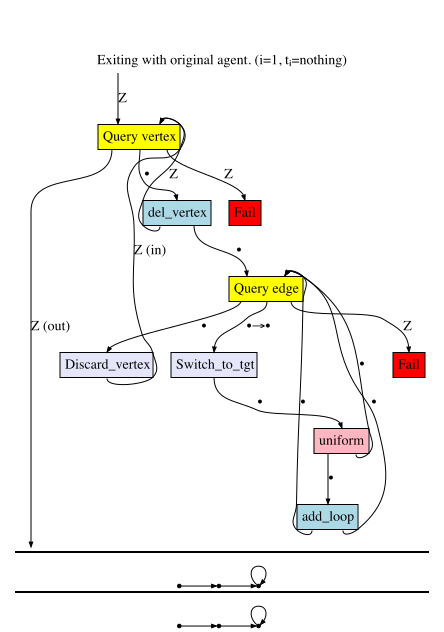
E.g. for each vertex \(v\):
AlgebraicJulia is a computational category-theoretic software ecosystem.
Catlab.jl defines the core data structures and algorithms with a focus on computing with presheaf categories. For example, consider the category Grph of presheaves on the schema (i.e. small category) \(E \rightrightarrows V\)
Rewrite and ControlFlow generatorsQuery, Weaken, Fail generators\[Ob_{\mathbf{Meal}} := Ob(\mathsf{Set})\] \[Hom_{\mathbf{Meal}}(A,B) := \left\{\left(S : \mathsf{Set},\ s_0 : S,\ \phi\colon A\times S\to S\times B\right)\right\}\]
Consider a case with \(S=1\), e.g. the rewrite rule add_loop as a morphism \(Grph \rightarrow Grph + Grph\):

A wire labeled by \(A \in Ob(\mathsf{C})\) represents the set \(Ob(A/\mathsf{\mathsf{C}}\text{-}\mathsf{Set})\).
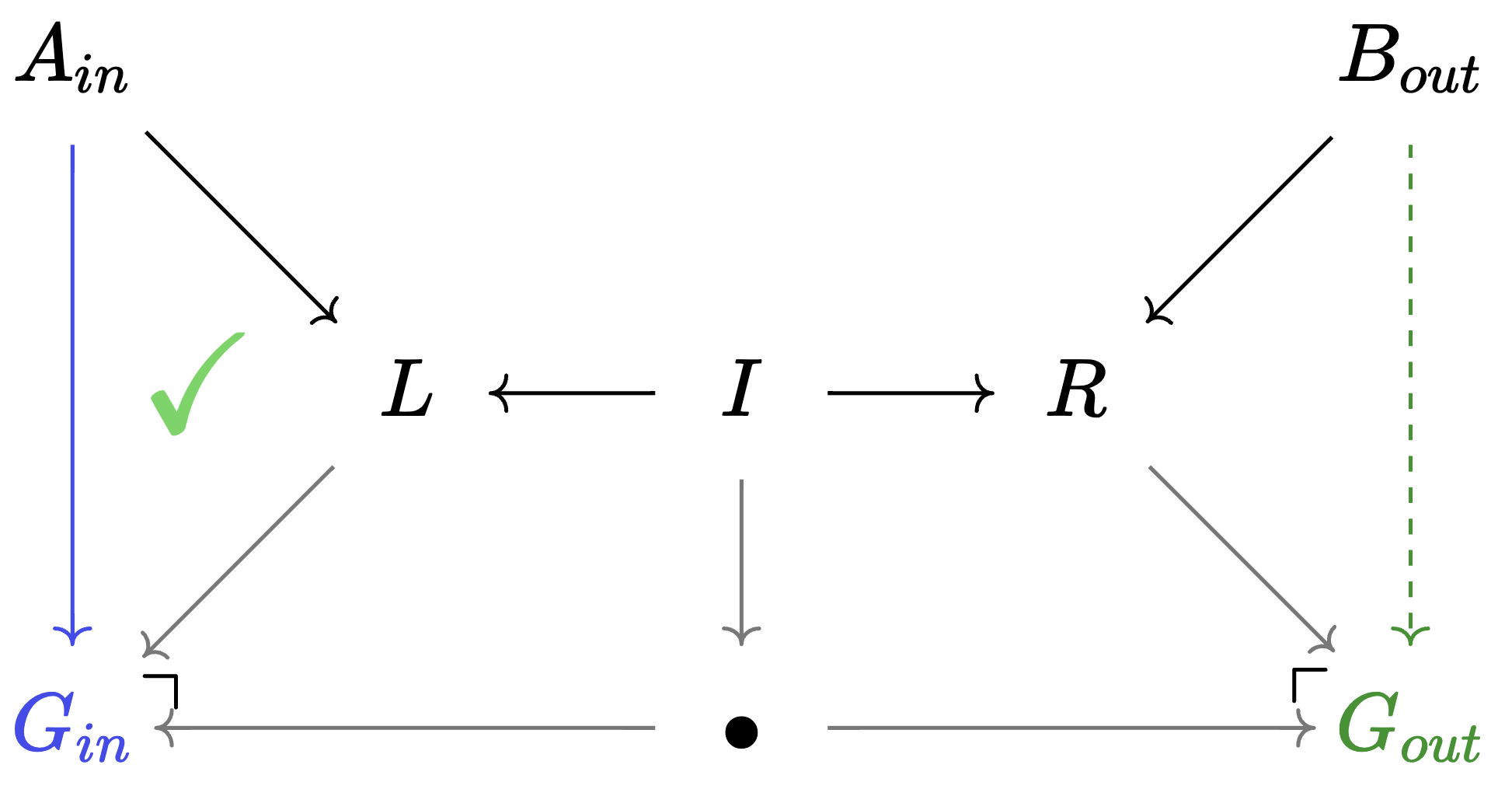
\(A\) is the shape of an agent living in a world \(X\) given by the morphism \(A \rightarrow X\). Being able to keep track of a distinguished subobject enables us to have control over matches.
Previously, the morphism add_loop had the semantics of ‘add a loop to some vertex’

With the ability to have distinguished agents, this morphism has the semantics of ‘add a loop to this vertex’.

Previously a Grph rewrite was \(Grph \rightarrow Grph + Grph\); now it is \(A/Grph \rightarrow B/Grph + A/Grph\) (in shorthand: \(A \rightarrow B + A\)).
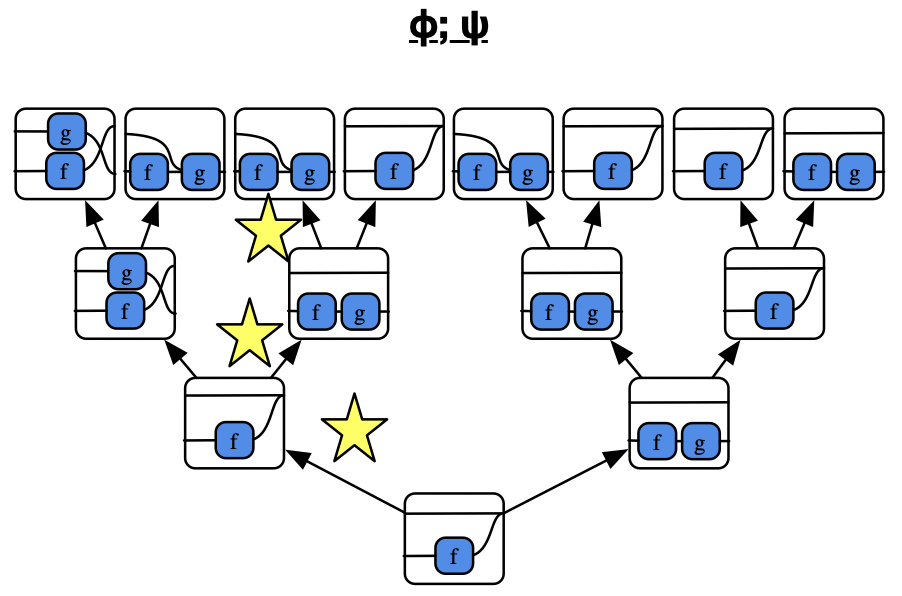
Control flow: consider a class of Mealy machines \(A \rightarrow A + A\) with \(S=\mathbb{N},s_0=3\) that acts as a for loop, by returning the first element iff \(s > 0\).

The Condition (or ControlFlow) primitive morphism is allowed to have nontrivial state but does not alter its inputs. Thus it must be a morphism \(A \rightarrow n \times A\).
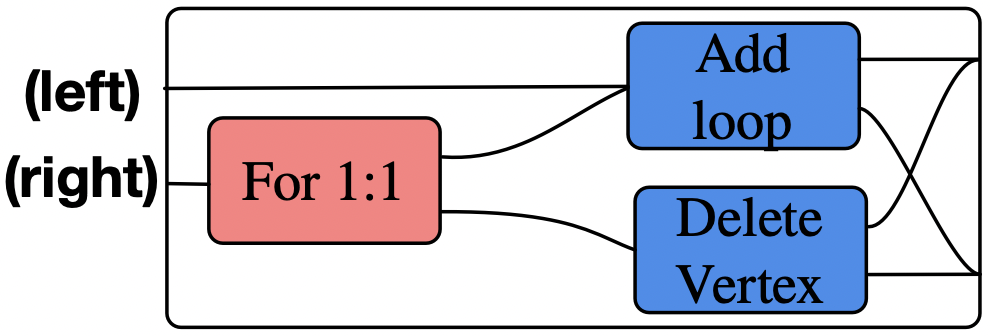
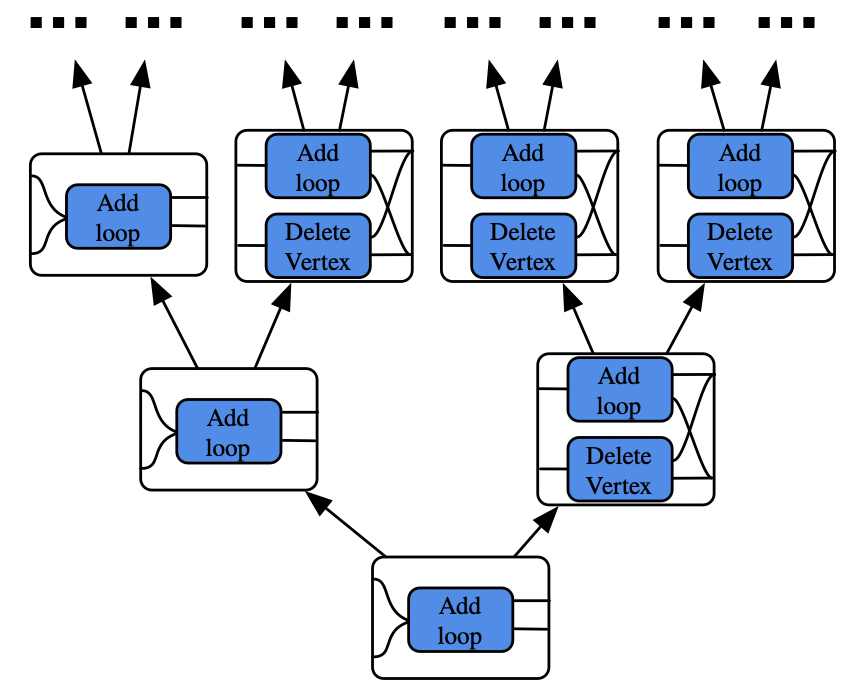
Let’s make a morphism which behaves like add_loop for the first three times the function is run and subsequently like delete_vertex:
\[ Grph \rightarrow Grph + Grph \] \[For3 \operatorname{⨟}(AddLoop \otimes DelVertex) \operatorname{⨟}(id_{Grph} \otimes \sigma_{Grph,Grph} \otimes id_{Grph}) \operatorname{⨟}\nabla_{Grph} \otimes \nabla_{Grph} \]
Our monoidal product \(\otimes\) comes from the coproduct in Set, but it is not a coproduct in Meal.
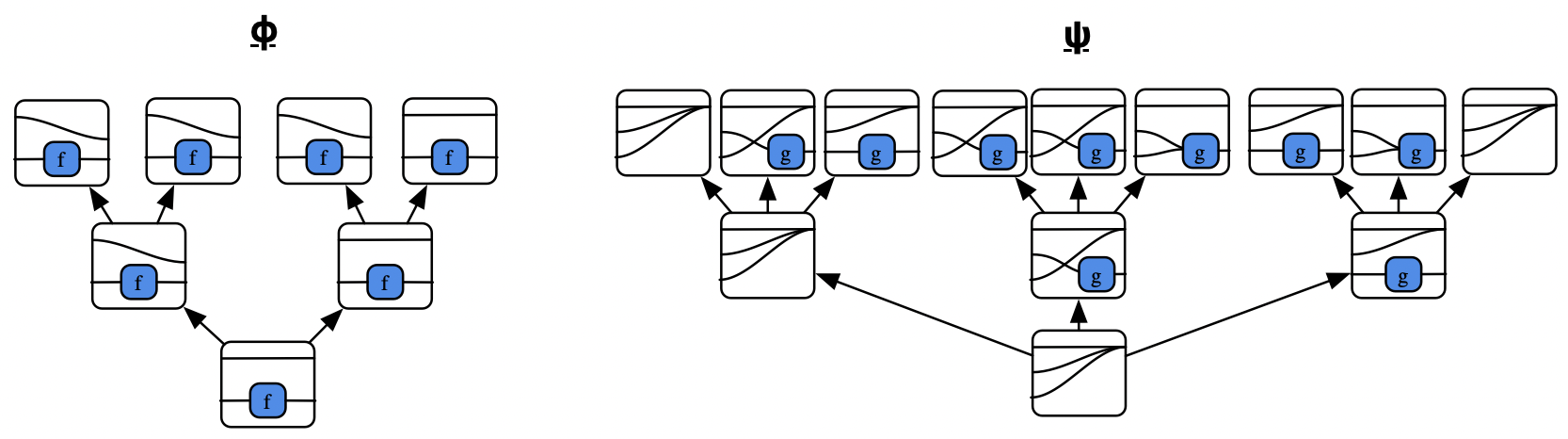
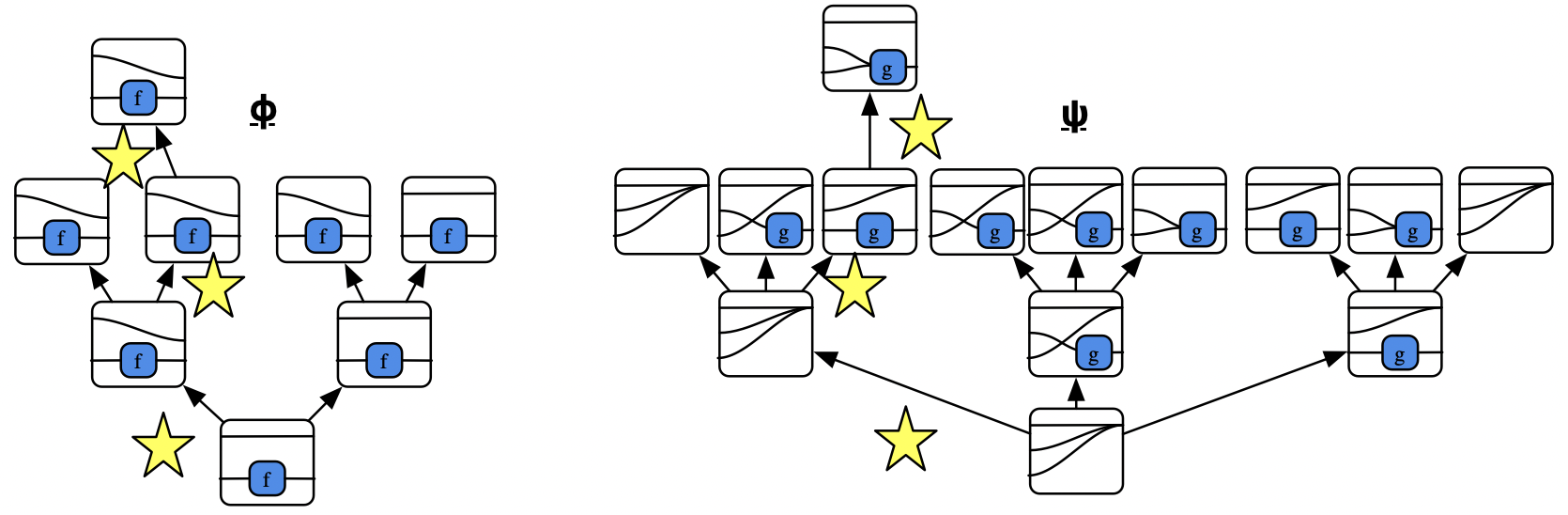
The behavior of a morphism \(A \rightarrow B\) is an infinite tree whose nodes are functions \(A \rightarrow B\) and which has a branching factor of \(A\).

Impractical to draw the behavior tree explicitly with infinite sets.
However, for a Mealy machine with domain \(\Sigma_i A_i\):
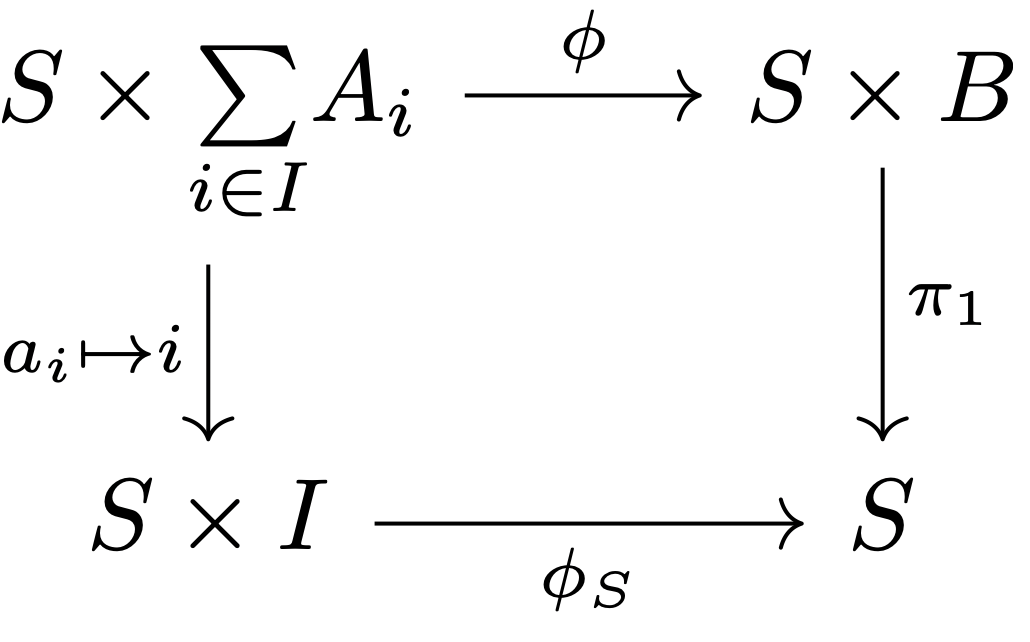
Consider this variant and its behavior tree:
Dict{Vector{BTreeEdge}, Any} with 1 entry:
[] => nothingWireVal(2, Traj(ACSetTransformation((V = FinFunction(Int64[], 0, 0), E = FinFunction(Int64[], 0, 0)), Graph {V = 0, E = 0}, Graph {V = 0, E = 0}), TrajStep[TrajStep(ACSetTransformation((V = FinFunction(Int64[], 0, 0), E = FinFunction(Int64[], 0, 0)), Graph {V = 0, E = 0}, Graph {V = 0, E = 0}), Multispan{Graph, StructTightACSetTransformation{TypeLevelBasicSchema{Symbol, Tuple{:V, :E}, Tuple{(:src, :E, :V), (:tgt, :E, :V)}, Tuple{}, Tuple{}}, NamedTuple{(:V, :E), Tuple{Catlab.CategoricalAlgebra.FinSets.FinDomFunctionVector{Int64, UnitRange{Int64}, Catlab.CategoricalAlgebra.FinSets.FinSetInt}, Catlab.CategoricalAlgebra.FinSets.FinDomFunctionVector{Int64, UnitRange{Int64}, Catlab.CategoricalAlgebra.FinSets.FinSetInt}}}, Graph, Graph}, StaticArraysCore.SVector{2, StructTightACSetTransformation{TypeLevelBasicSchema{Symbol, Tuple{:V, :E}, Tuple{(:src, :E, :V), (:tgt, :E, :V)}, Tuple{}, Tuple{}}, NamedTuple{(:V, :E), Tuple{Catlab.CategoricalAlgebra.FinSets.FinDomFunctionVector{Int64, UnitRange{Int64}, Catlab.CategoricalAlgebra.FinSets.FinSetInt}, Catlab.CategoricalAlgebra.FinSets.FinDomFunctionVector{Int64, UnitRange{Int64}, Catlab.CategoricalAlgebra.FinSets.FinSetInt}}}, Graph, Graph}}}(Graph:
V = 1:0
E = 1:0
src : E → V = Int64[]
tgt : E → V = Int64[], StructTightACSetTransformation{TypeLevelBasicSchema{Symbol, Tuple{:V, :E}, Tuple{(:src, :E, :V), (:tgt, :E, :V)}, Tuple{}, Tuple{}}, NamedTuple{(:V, :E), Tuple{Catlab.CategoricalAlgebra.FinSets.FinDomFunctionVector{Int64, UnitRange{Int64}, Catlab.CategoricalAlgebra.FinSets.FinSetInt}, Catlab.CategoricalAlgebra.FinSets.FinDomFunctionVector{Int64, UnitRange{Int64}, Catlab.CategoricalAlgebra.FinSets.FinSetInt}}}, Graph, Graph}[ACSetTransformation((V = FinFunction(1:0, 0, 0), E = FinFunction(1:0, 0, 0)), Graph {V = 0, E = 0}, Graph {V = 0, E = 0}), ACSetTransformation((V = FinFunction(1:0, 0, 0), E = FinFunction(1:0, 0, 0)), Graph {V = 0, E = 0}, Graph {V = 0, E = 0})]))]))\[Ob_{\mathbf{Meal/\sim}} := Ob(\mathsf{Set})\] \[Hom_{\mathbf{Meal/\sim}}(A,B) := Ob(\mathfrak{c}([Ay,By]))\]
\[Ob_{\mathbf{DynMeal}} := Ob(\mathsf{Set})\] \[Hom_{\mathbf{DynMeal}}(A,B) := \mathfrak{c}([Ay,By])\]
Where
The set of behavior trees is in bijection with the underlying set of the final coalgebra on \(X \rightarrow B^AX^A\). But we prefer to think about the category of morphisms \(A \rightarrow B\):
\[Ob_{\mathbf{DK_t}} := Ob(\mathsf{Set})\] \[Hom_{\mathbf{DK_t}}(A,B) := \mathfrak{c}([Ay,t \triangleleft By])\]
We can readily generalize our notion of a morphism \(A \rightarrow B\).
\[Maybe = y+1\]
\[Writer = My\]
\[List = \sum_{N : \mathbb{N}} y^N\]
\[Lott = \sum_{N : \mathbb{N}} \Delta_N y^N\]
where \(M\) is a monoid and \(\Delta_N:=\{P:N\rightarrow [0,1]\ |\ 1=\sum P(i)\}\)
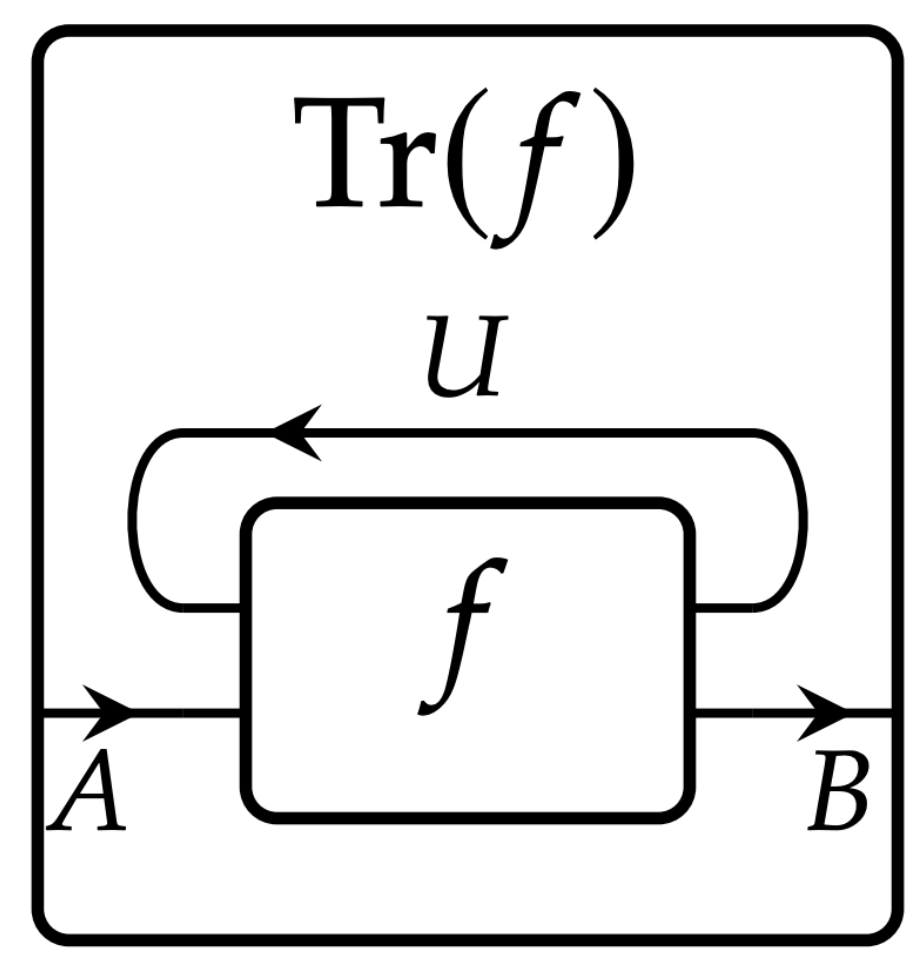

A trace structure licenses a graphical syntax with feedback loops.
Even without proving the purported trace structure, the theory has influenced an implementation.



A trace structure licenses a graphical syntax with feedback loops.
Even without proving the purported trace structure, the theory has influenced an implementation.
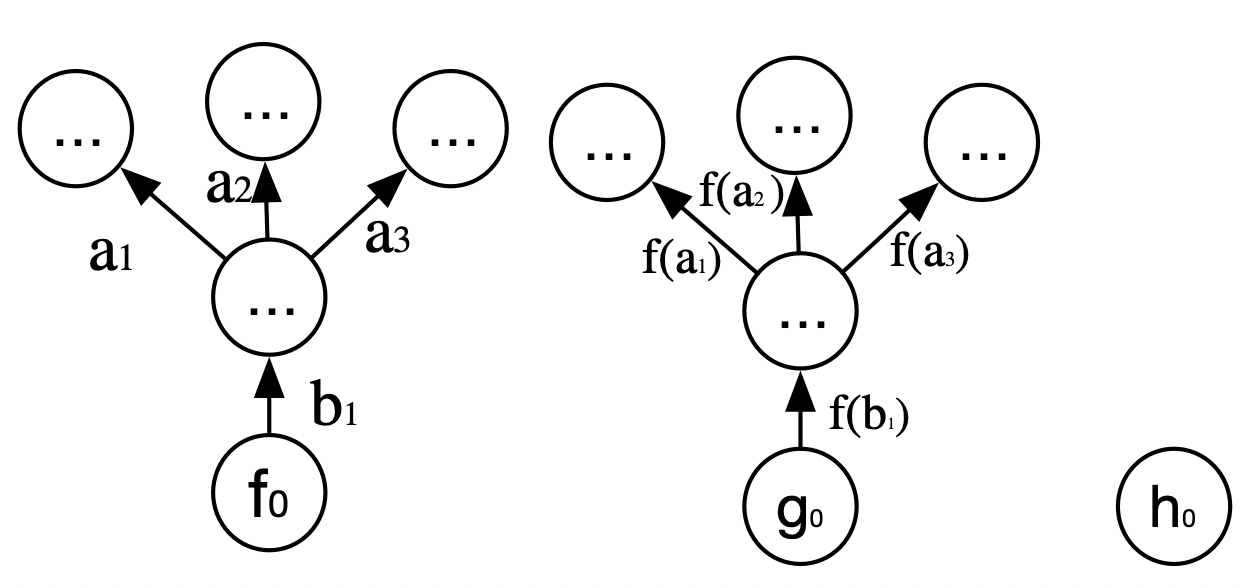
Poly morphisms are forwards on positions (trees) and backwards on directions (ways of updating): composition builds larger trees from smaller ones and decomposes updates of the larger system into corresponding updates of the smaller systems.
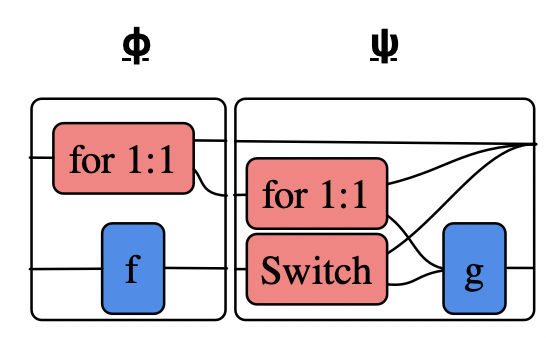
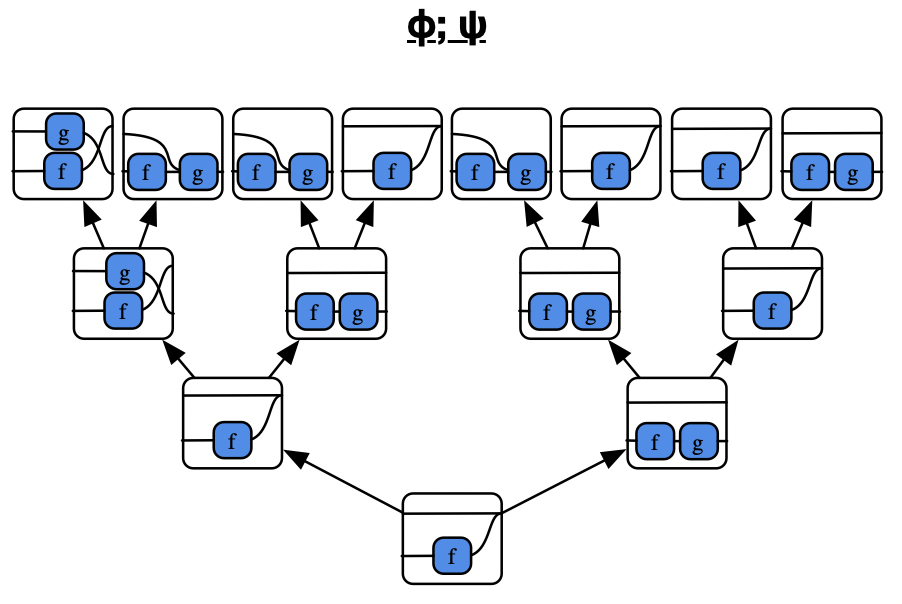

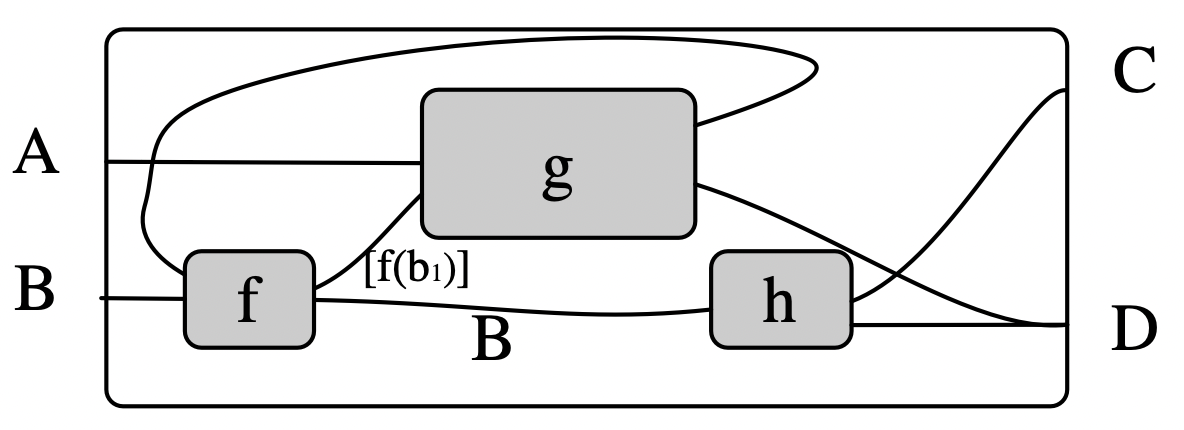
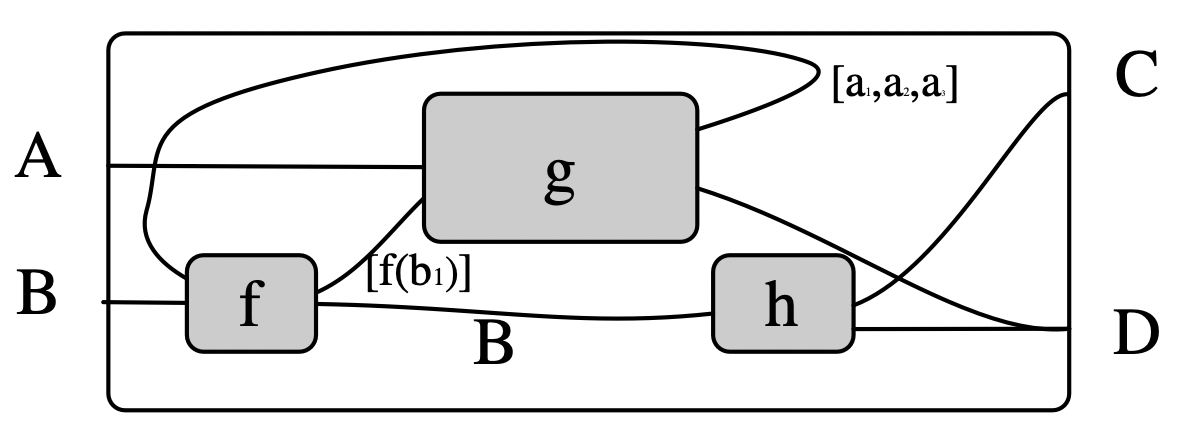
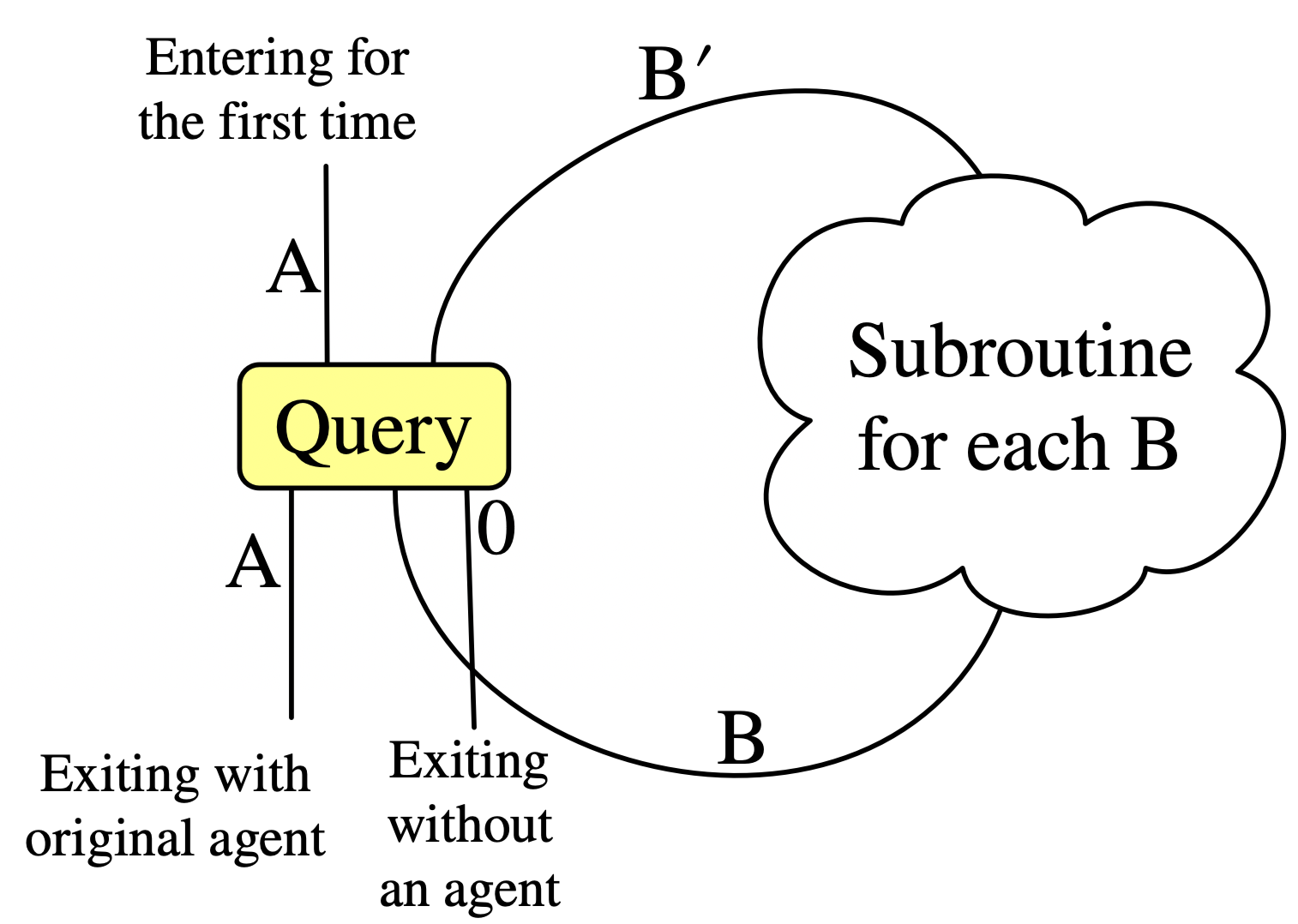
Although RuleApp and ControlFlow are the workhorse generators, we need others to facilitate the changing of control from agent to agent. Consider the Query morphism \(A + B' \rightarrow A + B + 0\), whose basic behavior is determined by the types \(A\) and \(B\) on its ports:
The last two generators of importance are Weaken and Fail. Both are stateless.
Weaken is a morphism \(B \rightarrow A\) and is specified by a morphism \(Hom_{C\mathsf{Set}}(A,B)\).

Fail is a morphism which throws the monadic exception.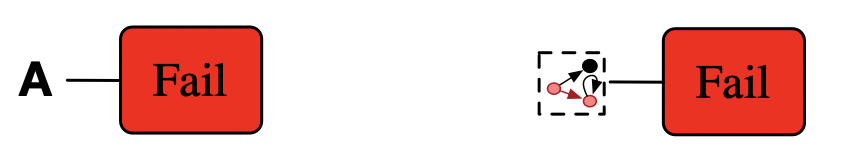
If \(v\) has no neighbors, delete it else…
\(\forall v\rightarrow v'\), if coin flip is heads, add a loop to \(v'\)
add_loop = RuleApp(:add_loop, Rule(id(G1), delete(G1)), G1);
del_vertex = RuleApp(:del_vertex, del_v, id(G1), id(G0))
per_edge = mk_sched((;),(i=Arr,), N,
(flip=uniform(2, Graph(1)), weak=Weaken(:Switch_to_tgt, t_hom), rule=add_loop),
quote
flip_yes, flip_no = flip(weak(i))
rule_yes, rule_no = rule(flip_yes)
return [flip_no, rule_yes, rule_no]
end
);
Much more to say about performance
Advantages from formalism
GCM 2023 paper: Dynamic Tracing: a graphical language for rewriting protocols
\[\text{Thank you for listening!}\]
What is a good syntax for talking about the algorithmic application of rewrite rules?
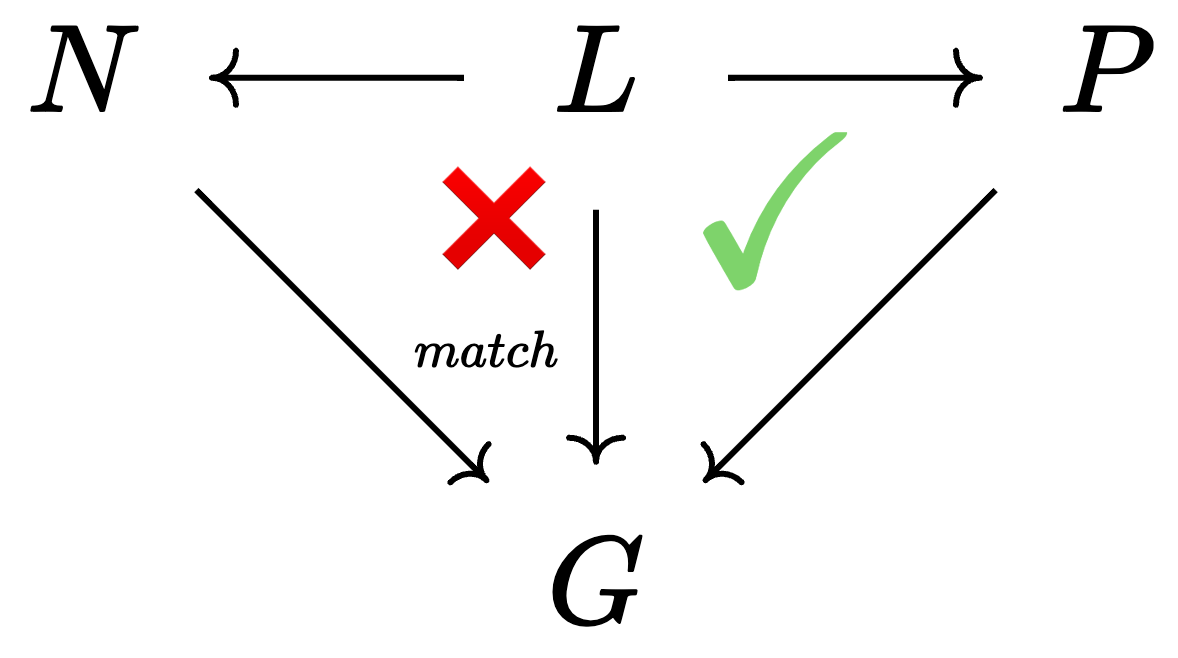
What is a good syntax for talking about the algorithmic application of rewrite rules?
What is a good syntax for talking about the algorithmic application of rewrite rules?
rewrite primatives


